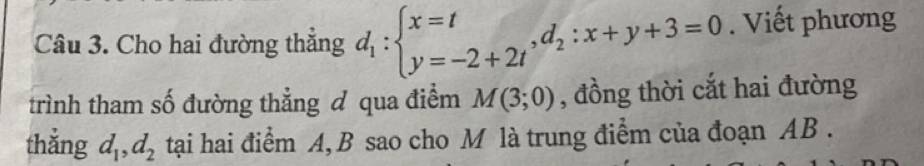Do A thuộc \(d_1\) nên tọa độ dạng \(A\left(a;-2+2a\right)\)
Do B thuộc \(d_2\) nên tọa độ dạng \(B\left(b;-b-3\right)\)
M là trung điểm AB nên: \(\left\{{}\begin{matrix}a+b=6\\-2+2a-b-3=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=6\\2a-b=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{11}{3}\\b=\dfrac{7}{3}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A\left(\dfrac{11}{3};\dfrac{16}{3}\right)\\B\left(\dfrac{7}{3};-\dfrac{16}{3}\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{AB}=\left(-\dfrac{4}{3};-\dfrac{32}{3}\right)=-\dfrac{4}{3}\left(1;8\right)\)
\(\Rightarrow\) Đường thẳng d nhận (1;8) là 1 vtcp
Phương trình d: \(\left\{{}\begin{matrix}x=3+t\\y=8t\end{matrix}\right.\)