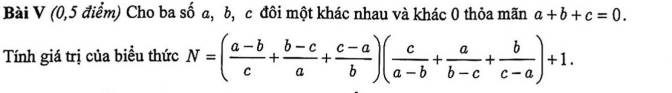Question

Answer 1

ĐK : \(a\ne b\ne c\ne0\)

Đặt \(x=\dfrac{a-b}{c};y=\dfrac{b-c}{a};z=\dfrac{c-a}{b}\)  (x;y;z \(\ne0\) )

Ta có : \(N=\left(x+y+z\right)\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)+1\)

\(=4+\dfrac{y+z}{x}+\dfrac{x+z}{y}+\dfrac{x+y}{z}\)

Thấy : \(\dfrac{y+z}{x}=\left(\dfrac{b-c}{a}+\dfrac{c-a}{b}\right).\dfrac{c}{a-b}=\dfrac{b-a}{ab}.\dfrac{c}{a-b}=\dfrac{-c}{ab}\)

Tương tự ; ta có : \(\dfrac{x+z}{y}=\dfrac{-a}{bc};\dfrac{x+y}{z}=-\dfrac{b}{ac}\)

Suy ra : \(N=4-\left(\dfrac{a}{bc}+\dfrac{b}{ac}+\dfrac{c}{ab}\right)=4-\dfrac{a+b+c}{abc}=4\)  ( do a + b + c = 0 ) 

Vậy ...