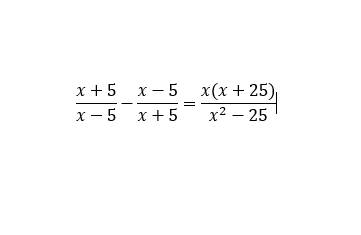\(\dfrac{x+5}{x-5}-\dfrac{x-5}{x+5}=\dfrac{x\left(x+25\right)}{x^2-25}\) ĐKXĐ : \(x^2-25\ne0\Leftrightarrow\left[{}\begin{matrix}x\ne-5\\x\ne5\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{x+5}{x-5}-\dfrac{x-5}{x+5}=\dfrac{x\left(x+25\right)}{\left(x-5\right)\left(x+5\right)}\)
\(\Leftrightarrow\dfrac{\left(x+5\right)^2}{\left(x-5\right)\left(x+5\right)}-\dfrac{\left(x-5\right)^2}{\left(x-5\right)\left(x+5\right)}=\dfrac{x\left(x+25\right)}{\left(x-5\right)\left(x+5\right)}\)
\(\Rightarrow\left(x+5\right)^2-\left(x-5\right)^2=x\left(x+25\right)\)
\(\Leftrightarrow x^2+10x+25-x^2+10x-25=x^2+25x\)
\(\Leftrightarrow20x=x^2+25x\)
\(\Leftrightarrow-x^2-25x+20x=0\)
\(\Leftrightarrow-x^2-5x=0\)
\(\Leftrightarrow x\left(-x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\-x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(KTM\right)\\x=-5\left(KTM\right)\end{matrix}\right.\)
⇒ Vô Nghiệm
\(\dfrac{x+5}{x-5}-\dfrac{x-5}{x+5}=\dfrac{x\left(x+25\right)}{x^2-25}\text{ĐKXĐ:}x\ne\pm5\)
\(\Leftrightarrow\dfrac{x+5}{x-5}-\dfrac{x-5}{x+5}=\dfrac{x\left(x+25\right)}{\left(x-5\right)\left(x+5\right)}\)
\(\Leftrightarrow\dfrac{\left(x+5\right)\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}-\dfrac{\left(x-5\right)\left(x-5\right)}{\left(x-5\right)\left(x+5\right)}=\dfrac{x\left(x+25\right)}{\left(x-5\right)\left(x+5\right)}\)
\(\Rightarrow x^2+5x+5x+25-x^2+5x+5x-25=x^2+25x\)
\(\Leftrightarrow20x=x^2+25x\)
\(\Leftrightarrow20x-x^2-25x=0\)
\(\Leftrightarrow-x^2-5x=0\)
\(\Leftrightarrow x\left(-x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\-x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\left(\text{loại}\right)\end{matrix}\right.\)
\(\text{Vậy phương trình có tập nghiệm là }S=\left\{0\right\}\)