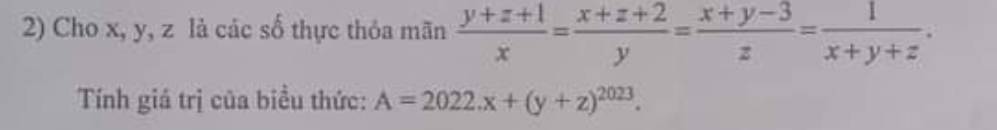Áp dụng t/c của dãy tỉ số bằng nhau , ta có
\(\dfrac{y+z+1}{x}=\dfrac{x+z+2}{y}=\dfrac{x+y-3}{z}=\dfrac{y+z+1+x+z+x+y-3}{x+y+z}\\ =\dfrac{2x+2y+2z}{x+y+z}=2\)
\(\Rightarrow\left\{{}\begin{matrix}y+z+1=2x\\x+z+2=2y\\x+y-3=2z\end{matrix}\right. \Rightarrow\left\{{}\begin{matrix}x+y+z+1=3x\\x+y+z+2=3y\\x+y+z-3=3z\end{matrix}\right.\)(*)
+, Từ đầu bài `=>(y+z+1)/x=1/(x+y+z)`
mà `(y+z+1)/x=2`
nên `1/(x+y+z)=2`
`=>x+y+z=1/2`
Thay `x+y+z=1/2` vào `(**)` , ta đc :
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{2}+1=3x\\\dfrac{1}{2}+2=3y\\\dfrac{1}{2}-3=3z\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{5}{6}\\z=-\dfrac{5}{6}\end{matrix}\right.\)
thay `x=1/2;y=5/6;z=-5/6` vào `A`, ta đc :
\(A=2022\cdot\dfrac{1}{2}+\left(\dfrac{5}{6}+\dfrac{-5}{6}\right)^{2023}\\ =1011+0=1011\)