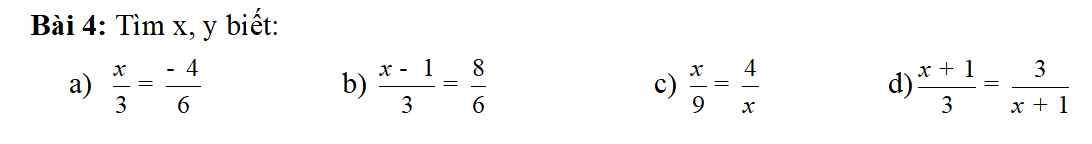\(a,\dfrac{x}{3}=-\dfrac{4}{6}\\ =>x=\dfrac{3\times\left(-4\right)}{6}=-2\\ b,\dfrac{x-1}{3}=\dfrac{8}{6}\\ =>6\left(x-1\right)=3.8\\ =>6x-6=24\\ =>6x=24+6\\ =>6x=30\\ =>x=30:6\\ =>x=5\\ c,\dfrac{x}{9}=\dfrac{4}{x}\\đk:x\ne0\\ =>x^2=36\\ =>\left[{}\begin{matrix}x=6\\x=-6\end{matrix}\right.\left(t/m\right)\\ d,\dfrac{x+1}{3}=\dfrac{3}{x+1}\\đk:x\ne -1\\ =>\left(x+1\right)\left(x+1\right)=9\\ =>x^2+x+x+1=9\\ =>x^2+2x-8=0\\ =>\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\left(t/m\right)\)
a)
`x/3=(-4)/6`
`=> x xx 6 = -4xx3`
`=> x xx 6 = -12`
`=> x=-12:6`
`=> x=-2`
b)
`(x-1)/3 = 8/6`
`=> (x-1)xx6=8xx3`
`=> (x-1)xx6=24`
`=> x-1=24:6`
`=> x-1=4`
`=> x=4+1`
`=> x=5`
c)
`x/9=4/x`
`=> x xx x = 4xx9`
`=> x^2=36`
\(\Rightarrow\left[{}\begin{matrix}x=6\\x=-6\end{matrix}\right.\)
d)
`(x+1)/3=3/(x+1)`
`=> (x+1)xx(x+1)=3xx3`
`=>(x+1)^2=9`
\(\Rightarrow\left[{}\begin{matrix}x+1=3\\x+1=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\)