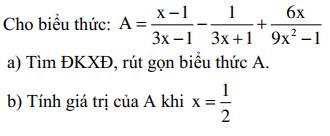a) ĐKXĐ: \(\left\{{}\begin{matrix}x\ne\dfrac{1}{3}\\x\ne-\dfrac{1}{3}\end{matrix}\right.\)
b) Với \(\left\{{}\begin{matrix}x\ne\dfrac{1}{3}\\x\ne-\dfrac{1}{3}\end{matrix}\right.\), ta có:
\(\Leftrightarrow\) A = \(\dfrac{\left(x-1\right)\left(3x+1\right)-\left(3x-1\right)+6x}{\left(3x+1\right)\left(3x-1\right)}\)
\(=\dfrac{3x^2+x-3x-1-3x+1+6x}{\left(3x+1\right)\left(3x-1\right)}\)
\(=\dfrac{3x^2+x}{\left(3x+1\right)\left(3x-1\right)}\)
\(=\dfrac{x\left(3x+1\right)}{\left(3x+1\right)\left(3x-1\right)}\)
\(=\dfrac{x}{3x-1}\)
Với \(\left\{{}\begin{matrix}x\ne\dfrac{1}{3}\\x\ne-\dfrac{1}{3}\end{matrix}\right.\), thay \(x=\dfrac{1}{2}\) vào A, ta có:
\(A=\left(\dfrac{1}{2}\right):\left(3\cdot\dfrac{1}{2}-1\right)\)
\(=\dfrac{1}{2}:\dfrac{1}{2}\) \(=1\)
\(A=\dfrac{x-1}{3x-1}-\dfrac{1}{3x+1}+\dfrac{6x}{9x^2-1}\left(đkxđ:x\ne\pm\dfrac{1}{3}\right)\)
\(=\dfrac{\left(x-1\right)\left(3x+1\right)-3x+1+6x}{\left(3x-1\right)\left(3x+1\right)}\)
\(=\dfrac{3x^2+x-3x-1-3x+1+6x}{\left(3x-1\right)\left(3x+1\right)}\)
\(=\dfrac{3x^2+x}{\left(3x-1\right)\left(3x+1\right)}\)
\(=\dfrac{x\left(3x+1\right)}{\left(3x-1\right)\left(3x+1\right)}\)
\(=\dfrac{x}{3x-1}\)
Vậy \(A=\dfrac{x}{3x-1}\)
Thay \(x=\dfrac{1}{2}\) vào A , ta được :
\(A=\dfrac{\dfrac{1}{2}}{3.\dfrac{1}{2}-1}=\dfrac{1}{4}\)
Vậy khi \(x=\dfrac{1}{2}\) thì \(A=\dfrac{1}{4}\)