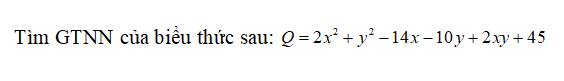Question

Answer 1

\(Q=2x^2+y^2-14x-10y+2xy+45\)

\(=y^2+2y\left(x-5\right)+\left(x-5\right)^2-\left(x-5\right)^2+2x^2-14x+45\)

\(=\left(y+x-5\right)^2+x^2-4x+20\)

\(=\left(y+x-5\right)^2+\left(x-2\right)^2+16\)

Vì \(\left\{{}\begin{matrix}\left(y+x-5\right)^2\ge0\forall x,y\\\left(x-2\right)^2\ge0\forall x\end{matrix}\right.\)

\(MinQ=16\Leftrightarrow\left\{{}\begin{matrix}x+y-5=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)