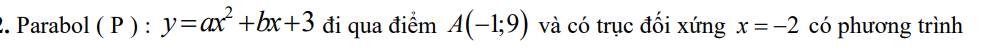\(\left(P\right):y=ax^2+bx+3\left(a\ne0\right)\)
\(\left(P\right)\) đi qua điểm \(A\left(-1;9\right)\Leftrightarrow a.\left(-1\right)^2+b.\left(-1\right)+3=9\Leftrightarrow a-b=6\left(1\right)\)
\(\left(P\right)\) có trục đối xứng \(x=-2\Leftrightarrow\dfrac{-b}{2a}=-2\Leftrightarrow-4a+b=0\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\left\{{}\begin{matrix}a-b=6\\-4a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-8\end{matrix}\right.\)
\(\Rightarrow\left(P\right):y=-2x^2-8x+3\)
Đúng 1
Bình luận (0)
