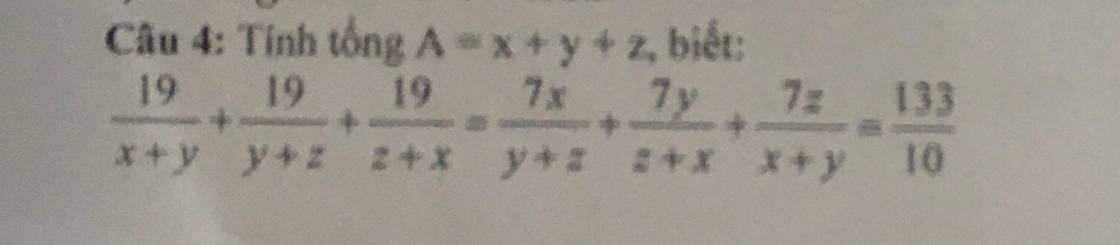Question

Answer 1

Lời giải:
Từ ĐKĐB suy ra:
$\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}=\frac{133}{10}: 19=\frac{133}{190}=\frac{7}{10}$

Lại có:

$\frac{7x}{y+z}+\frac{7y}{z+x}+\frac{7z}{x+y}=\frac{133}{10}$

$\Leftrightarrow \frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}=\frac{133}{10}: 7=\frac{19}{10}$

$\Leftrightarrow \frac{x}{y+z}+1+\frac{y}{z+x}+1+\frac{z}{x+y}+1=\frac{19}{10}+3=\frac{49}{10}$

$\Leftrightarrow \frac{x+y+z}{y+z}+\frac{x+y+z}{z+x}+\frac{x+y+z}{x+y}=\frac{49}{10}$

$\Leftrightarrow (x+y+z)(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x})=\frac{49}{10}$

$\Leftrightarrow A.\frac{7}{10}=\frac{49}{10}$

$\Leftrightarrow A=7$