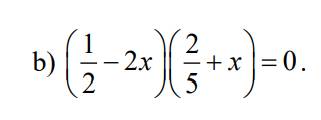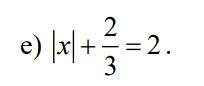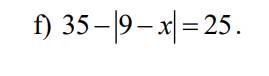Question

Answer 1

b)

\(\left(\dfrac{1}{2}-2x\right)\left(\dfrac{2}{5}+x\right)=0\\ \left[{}\begin{matrix}\dfrac{1}{2}-2x=0\\\dfrac{2}{5}+x=0\end{matrix}\right.\\ \left[{}\begin{matrix}2x=\dfrac{1}{2}\\x=-\dfrac{2}{5}\end{matrix}\right.\left[{}\begin{matrix}x=\dfrac{1}{4}\\x=-\dfrac{2}{5}\end{matrix}\right.\)

e)

\(\left|x\right|+\dfrac{2}{3}=2\\ \left|x\right|=2-\dfrac{2}{3}\\ \left|x\right|=\dfrac{4}{3}\\ \left[{}\begin{matrix}x=\dfrac{4}{3}\\x=-\dfrac{4}{3}\end{matrix}\right.\)

f)

\(35-\left|9-x\right|=25\\ \left|9-x\right|=35-25\\ \left|9-x\right|=10\\ \left[{}\begin{matrix}9-x=10\\9-x=-10\end{matrix}\right.\\ \left[{}\begin{matrix}x=9-10\\x=9-\left(-10\right)\end{matrix}\right.\\ \left[{}\begin{matrix}x=-1\\x=19\end{matrix}\right.\)

Answer 2