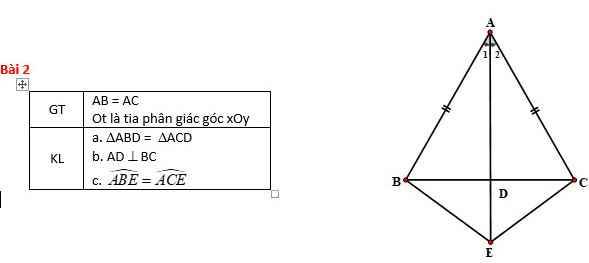
Sửa GT: `AD` là tia phân giác của `\hat{BAC}`
`a)` Vì `Ot` là tia phân giác của `\hat{BAC}=>\hat{A_1}=\hat{A_2}`
Xét `\triangle ABD` và `\triangle ACD` có:
`{:(AB=AC),(\vec{A_1}=\hat{A_2}),(AD\text{ là cạnh chung}):}}=>`
`=>\triangle ABD =\triangle ACD` (c-g-c)
`b)` Vì `\triangle ABD =\triangle ACD=>\hat{ADB}=\hat{ADC}`
Ta có: `\hat{ADB}+\hat{ADC}=180^o`
`=>2\hat{ADB}=180^o =>\hat{ADB}=90^o`
`=>AD \bot BD` hay `AD \bot BC` tại `D`
`c)` Xét `\triangle ABE` và `\triangle ACE` có:
`{:(AB=AC),(\hat{A_1}=\hat{A_2}),(AE\text{ là cạnh chung}):}}=>`
`=>\triangle ABE=\triangle ACE` (c-g-c)
`=>\hat{ABE}=\hat{ACE}`