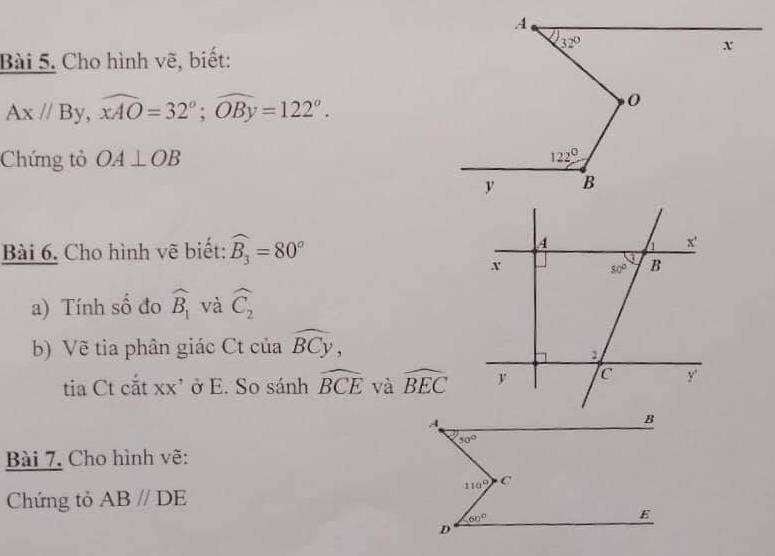
bài 5: Qua O, vẽ Oz // By // Ax (bạn tự kẻ nha)
Ta có: \(\widehat{A}=\widehat{AOz}=32^0\) (2 góc sole trong)
\(\widehat{B}+\widehat{BOz}=180^0\) (2 góc trong cùng phía bù nhau)
\(122^0+\widehat{BOz}=180^0\)
\(\Rightarrow\)\(\widehat{BOz}=58^0\)
Mà \(\widehat{AOB}=\widehat{AOz}+\widehat{BOz}\)
\(\Rightarrow\) \(\widehat{AOB}=32^0+58^0\)
\(\Rightarrow\)\(\widehat{AOB}=90^0\)
\(\Rightarrow\) OA \(\perp\) OB
bài 6:
Ta có: \(\widehat{B_1}=\widehat{B_3}=50^0\) (2 góc đối đỉnh)
\(\widehat{B_1}=\widehat{BCy'}=50^0\) (2 góc sole trong)
\(\widehat{BCy'}+\widehat{C_2}=180^0\) (2 góc kề bù)
\(\Rightarrow\) \(50^0+\widehat{C_2}=180^0\)
\(\Rightarrow\)\(\widehat{C_2}=130^0\)
b, (bạn cũng tự vẽ hình nha)
vì CT là tia phân giác của \(\widehat{BCy}\)
\(\Rightarrow\) \(\widehat{BCE}= \dfrac {1} {2} \widehat{BCy}\)
\(\Rightarrow \widehat{BCE}=65^0\)
vì CT cắt đt xx' nên CT cũng là tia phân giác của góc \(\widehat{A}\)
\(\Rightarrow\) \(\widehat{BEC}= \dfrac {1} {2} \widehat{A}\)
\(\Rightarrow\)\(\widehat{BEC}=45^0\)
\(\Rightarrow \widehat{BCE} (65^0)>\widehat{BEC}(45^0)\)