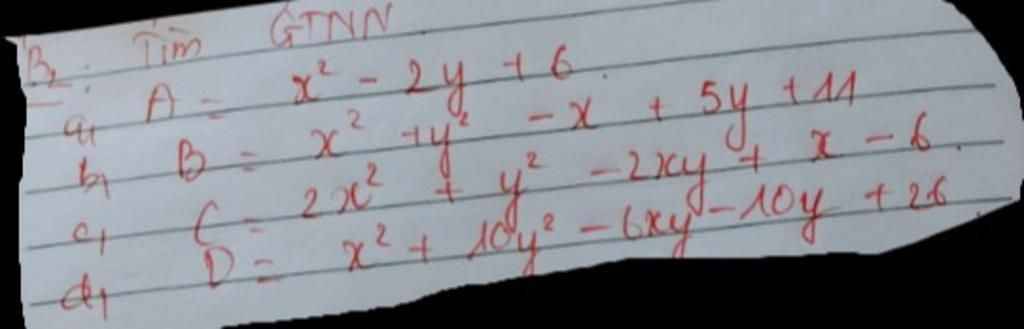\(A=x^2-2x+6=x^2-2x+1+5\ge5\)
Dấu "=" xảy ra khi \(x=1\)
\(B=x^2+y^2-x+5y+11=x^2-2.x.\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{4}+y^2+2.y.\dfrac{5}{2}+\dfrac{25}{4}-\dfrac{25}{4}+11\)
\(B=\left(x-\dfrac{1}{2}\right)^2+\left(y+\dfrac{5}{2}\right)^2+\dfrac{9}{2}\ge\dfrac{9}{2}\)
Dấu "=" xảy khi \(\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-\dfrac{5}{2}\end{matrix}\right.\)
\(C=2x^2+y^2-2xy+x-6=x^2-2xy+y^2+x^2+2.x.\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{4}-6\)
\(C=\left(x-y\right)^2+\left(x+\dfrac{1}{2}\right)^2-\dfrac{25}{4}\ge-\dfrac{25}{4}\)
dấu "=" xảy ra khi \(x=y=-\dfrac{1}{2}\)
\(D=x^2+10y^2-6xy-10y+26=x^2-6xy+9y^2+y^2-10y+25+1\)
\(D=\left(x-3y\right)^2+\left(y-5\right)^2+1\ge1\)
dấu "=" xảy ra khi \(\left\{{}\begin{matrix}x=15\\y=5\end{matrix}\right.\)