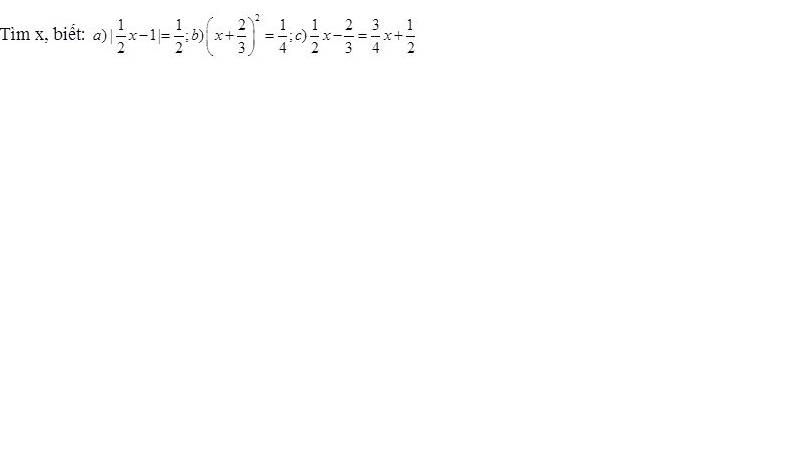a, \(\left[{}\begin{matrix}\dfrac{1}{2}x-1=\dfrac{1}{2}\\\dfrac{1}{2}x-1=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
b, \(\left[{}\begin{matrix}x+\dfrac{2}{3}=\dfrac{1}{2}\\x+\dfrac{2}{3}=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{6}\\x=-\dfrac{7}{6}\end{matrix}\right.\)
c, \(\dfrac{1}{2}x-\dfrac{3}{4}x=\dfrac{1}{2}+\dfrac{2}{3}=\dfrac{7}{6}\Leftrightarrow\dfrac{-1}{4}x=\dfrac{7}{6}\Leftrightarrow x=\dfrac{7}{6}\left(-4\right)=\dfrac{-28}{6}=-\dfrac{14}{3}\)
`|1/2 x-1| = 1/2`
`@TH1:`
`1/2x-1 = 1/2`
`1/2 x = 1/2+1`
`1/2 x= 1/2+2/2`
`1/2 x = 3/2`
`x=3/2:1/2`
`x=3/2 xx 2`
`x=3`
`@TH2:`
`1/2x - 1 = -1/2`
`1/2x =-1/2+1`
`1/2x = -1/2+2/2`
`1/2x = 1/2`
`x=1/2:1/2`
`x=1/2 xx 2`
`x=1`
_______________________________
`(x+2/3)^2 = 1/4`
\(\left(x+\dfrac{2}{3}\right)^2=\left(\pm\dfrac{1}{2}\right)^2\)
`@Th1:`
`x+2/3=1/2`
`x=1/2-2/3`
`x=3/6 - 4/6`
`x=-1/6`
`@Th2:`
`x+2/3=-1/2`
`x=-1/2-2/3`
`x=-3/6-4/6`
`x=-7/6`
Vậy `x={-7/6 ; -1/6}`
______________________________
`1/2x-2/3 = 3/4x +1/2`
`1/2x -3/4x = 2/3+1/2`
` 1/2x -3/4x = 4/6 +3/6`
`1/2x -3/4x = 7/6`
`(1/2 - 3/4)x=7/6`
`(2/4 - 3/4)x=7/6`
`-1/4x = 7/6`
`x=7/6:(-1/4)`
`x=7/6 xx (-4)`
`x=-14/3`
Vậy `x=-14/3`