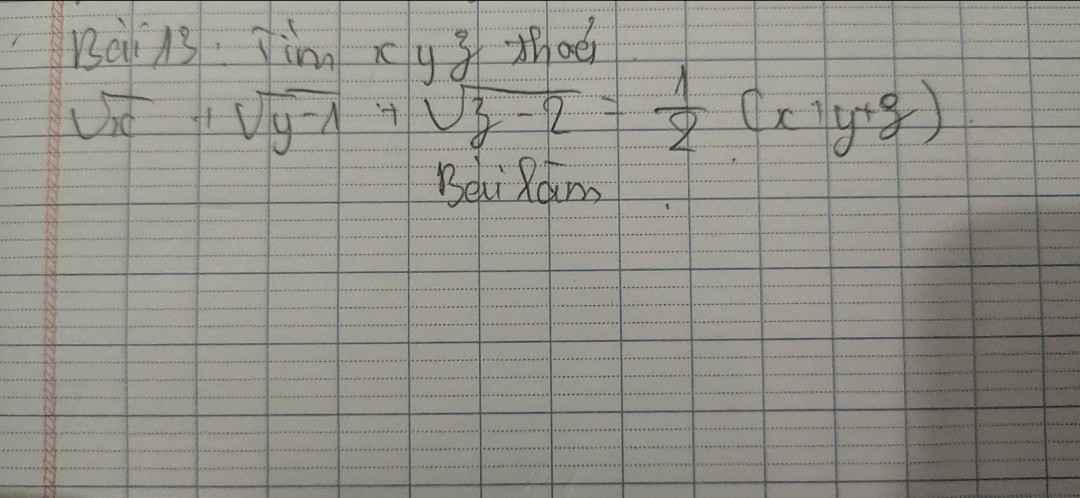Question

Answer 1

Điều kiện: \(x\ge0;y\ge1;z\ge2\)

\(\sqrt{x}+\sqrt{y-1}+\sqrt{z-2}=\dfrac{1}{2}\left(x+y+z\right)\\ \Rightarrow2\sqrt{x}+2\sqrt{y-1}+2\sqrt{z-2}=x+y+z\\\Rightarrow \left(x-2\sqrt{x}+1\right)+\left(y-1-2\sqrt{y-1}+1\right)+\left(z-2-2\sqrt{z-2}+1\right)=0\\\Rightarrow \left(\sqrt{x}-1\right)^2+\left(\sqrt{y-1}-1\right)^2+\left(\sqrt{z-2}-1\right)^2=0\\\Rightarrow \left\{{}\begin{matrix}\sqrt{x}-1=0\\\sqrt{y-1}-1=0\\\sqrt{z-2}-1=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x=1\\y-1=1\\z-2=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=1\\y=2\\z=3\end{matrix}\right.\left(TM\right)\)