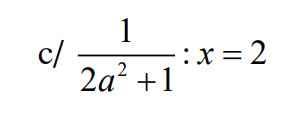Question

Answer 1

\(\dfrac{1}{2a^2+1}:x=2\\ \dfrac{1}{2a^2+1}.\dfrac{1}{x}=2\\ \dfrac{1}{\left(2a^2+1\right).x}=2\\ \left(2a^2+1\right).x=\dfrac{1}{2}\\ x=\dfrac{1}{2.\left(2a^2+1\right)}\\ x=\dfrac{1}{4a^2+2}\)

Vậy \(x=\dfrac{1}{4a^2+2}\)

Với a là hằng số

Answer 2

\(\dfrac{1}{2a^2+1}:x=2\)

\(\dfrac{1}{2a^2+1}=2\cdot x\)

\(x=\dfrac{1}{2a^2+1}:2\)

\(x=\dfrac{1}{2\left(2a^2+1\right)}=\dfrac{1}{4a^2+2}\)

Vậy \(x=\dfrac{1}{4a^2+2}\) với a đóng vai trò là hằng số