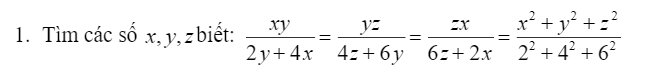Xét \(x=0\Rightarrow y=0,z=0\Rightarrow2y+4z=0\) (vô lý)
Suy ra \(x\ne0;y\ne0;z\ne0\)
Khi đó từ đề suy ra:
\(\dfrac{2y+4x}{xy}=\dfrac{4z+6y}{yz}=\dfrac{6x+2z}{zx}=\dfrac{2^2+4^2+6^2}{x^2+y^2+z^2}\)
\(\Rightarrow\dfrac{2}{x}+\dfrac{4}{y}=\dfrac{4}{y}+\dfrac{6}{z}=\dfrac{6}{z}+\dfrac{2}{x}=\dfrac{2^2+4^2+6^2}{x^2+y^2+z^2}\)
Đặt \(\dfrac{2}{x}=\dfrac{4}{y}=\dfrac{6}{z}=\dfrac{1}{k}\left(k\ne0\right)\) thì \(\dfrac{2^2+4^2+6^2}{x^2+y^2+z^2}=\dfrac{2}{k}\)
Suy ra: \(x=2k;y=4k;z=6k\) và \(x^2+y^2+z^2=28k\left(3\right)\)
Thay \(x=2k,y=4k,z=6k\) vào (3) ta được:
\(\left(2k\right)^2+\left(4k\right)^2+\left(6k\right)^2=28k\)
\(\Rightarrow56k^2-28k=0\Rightarrow\left[{}\begin{matrix}k=0\left(ktm\right)\\k=\dfrac{1}{2}\left(tm\right)\end{matrix}\right.\)
Với \(k=\dfrac{1}{2}\Rightarrow x=1;y=2;z=3\)
Vậy \(x=1;y=2;z=3\)