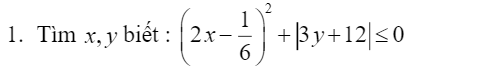Vì
\(\left(2x-\dfrac{1}{6}\right)^2\ge0\forall x\)
\(\left|3y+12\right|\ge0\forall y\)
\(\Rightarrow\left(2x-\dfrac{1}{6}\right)^2+\left|3y+12\right|\ge0\)
Mà đề cho \(\left(2x-\dfrac{1}{6}\right)^2+\left|3y+12\right|\le0\Rightarrow\left(2x-\dfrac{1}{6}\right)^2+\left|3y+12\right|=0\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}2x-\dfrac{1}{6}=0\\3y+12=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{12}\\y=-4\end{matrix}\right.\)
Vậy \(\left(x,y\right)=\left(\dfrac{1}{12};-4\right)\)
Đúng 3
Bình luận (0)