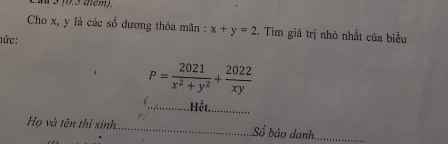-Áp dụng BĐT AM-GM cho 2 số dương ta có:
\(2\sqrt{xy}\le x+y\)
\(\Leftrightarrow4xy\le\left(x+y\right)^2\)
\(\Leftrightarrow xy\le\dfrac{\left(x+y\right)^2}{4}=\dfrac{2^2}{4}=1\)
\(P=\dfrac{2021}{x^2+y^2}+\dfrac{2022}{xy}=\dfrac{2021}{x^2+y^2}+\dfrac{2021}{2xy}+\dfrac{2023}{2xy}=2021.\left(\dfrac{1}{x^2+y^2}+\dfrac{1}{2xy}\right)+\dfrac{2023}{2xy}\)-Áp dụng BĐT Caushy Schwarz ta có:
\(P=2021.\left(\dfrac{1}{x^2+y^2}+\dfrac{1}{2xy}\right)+\dfrac{2023}{2xy}\ge2021.\dfrac{\left(1+1\right)^2}{x^2+y^2+2xy}+\dfrac{2023}{2.1}=2021.\dfrac{4}{\left(x+y\right)^2}+\dfrac{2023}{2}=2021.\dfrac{4}{2^2}+\dfrac{2023}{2}=\dfrac{6065}{2}\)\(P=\dfrac{6065}{2}\Leftrightarrow x=y=1\)
-Vậy \(P_{min}=\dfrac{6065}{2}\)