a) Xét △ vuông ABE và △ vuông HBE (\(\widehat{BAE}\) = \(\widehat{BHE}\) = 90o) ta có:
AE = BH (gt)
\(\widehat{B}\)1 = \(\widehat{B}\)2 (gt)
⇒ △ vuông ABE = △ vuông HBE (ch - gn)
mai em thi cuối kì rồi giúp em vs ạk
1) xét △ABE và △HBE, ta có:
- B1 = B2
- BE cạnh chung
- góc A = góc C
=> △ABE = △HBE
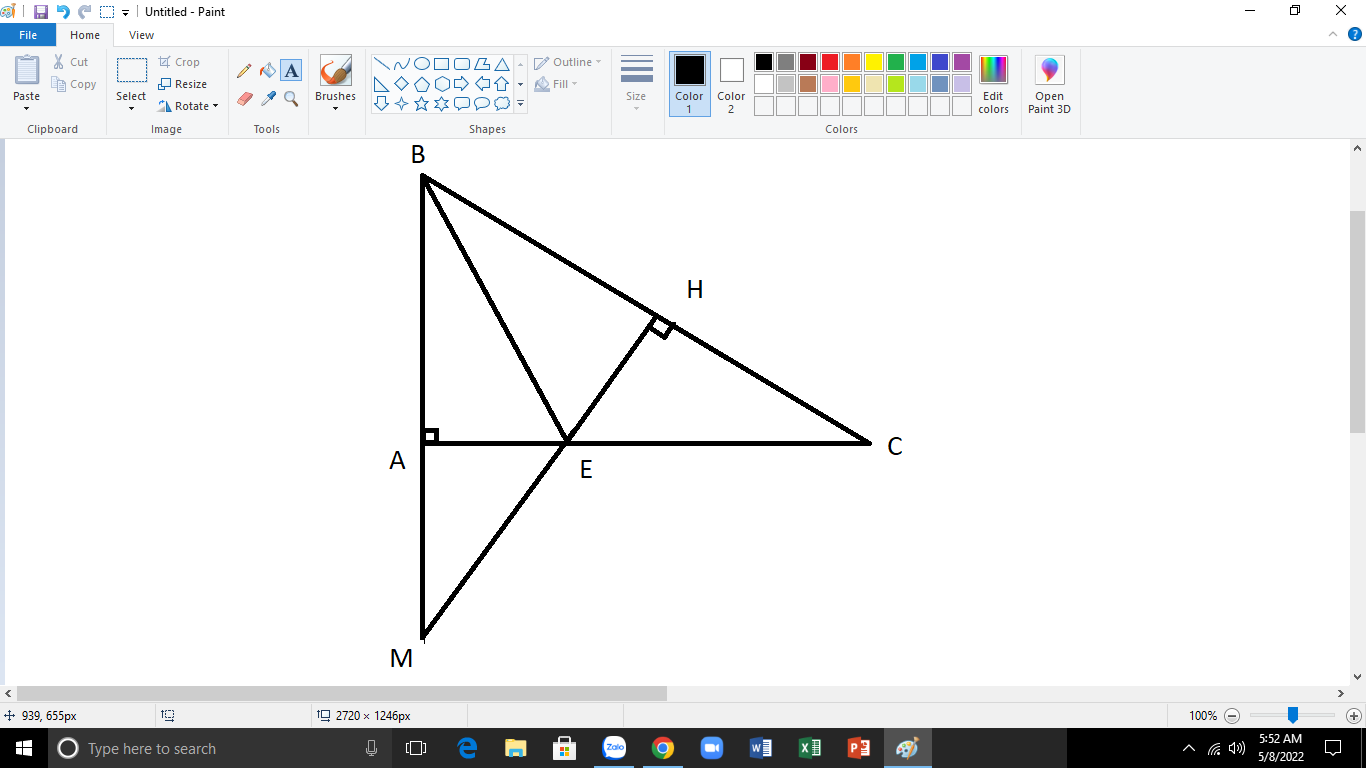
\(\text{a)Xét }\Delta ABE\text{ và }\Delta HBE\text{ có:}\)
\(\widehat{BAE}=\widehat{BHE}=90^0\left(gt\right)\)
\(BE\text{ chung}\)
\(\widehat{ABE}=\widehat{HBE}\left(BE\text{ là phân giác }\widehat{B}\right)\)
\(\Rightarrow\Delta ABE=\Delta HBE\left(ch-gn\right)\)
\(\text{b)Xét }\Delta AEM\text{ và }\Delta HEC\text{ có:}\)
\(\widehat{MAE}=\widehat{CHE}=90^0\left(gt\right)\)
\(AE=HE\left(\Delta ABE=\Delta HBE\right)\)
\(\widehat{AEM}=\widehat{HEC}\left(\text{đối đỉnh}\right)\)
\(\Rightarrow\Delta AEM=\Delta HEC\left(g-c-g\right)\)
\(\Rightarrow EM=EC\left(\text{hai cạnh tương ứng}\right)\)
\(\text{c)Ta có:AB=HB}\left(\Delta ABE=\Delta HBE\right)\)
\(\text{Mà AM=HC}\left(\Delta AEM=\Delta HEC\right)\)
\(\Rightarrow BM=BC\)
\(\text{Xét }\Delta BHM\text{ vuông tại H có:}\)
\(\text{BM là cạnh huyền lớn nhất}\)
\(\Rightarrow BM>MH\left(1\right)\)
\(\text{Mà BM=BC(cmt)}\)
\(\Rightarrow BC>MH\)


















