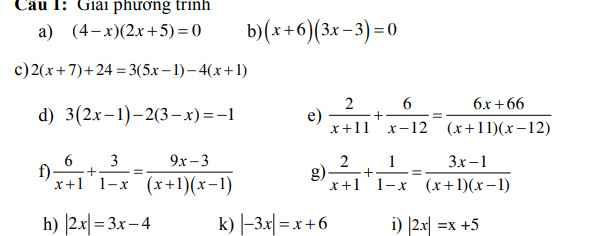a) (\(4\) - \(x\)).(\(2x\) + \(5\)) = 0
⇔ \(\left[{}\begin{matrix}4-x=0\\2x+5=0\end{matrix}\right.\) ⇔\(\left[{}\begin{matrix}x=4-0\\2x=0-5\end{matrix}\right.\)⇔ \(\left[{}\begin{matrix}x=4\\x=-\dfrac{5}{2}\end{matrix}\right.\)
Vậy: ..........
b) (x + 6)(3x - 3) = 0
⇔\(\left[{}\begin{matrix}x+6=0\\3x-3=0\end{matrix}\right.\) ⇔\(\left[{}\begin{matrix}x=0-6\\3x=0+3\end{matrix}\right.\)⇔\(\left[{}\begin{matrix}x=-6\\x=1\end{matrix}\right.\)
Vậy: .........
c) 2(x + 7) + 24 = 3(5x - 1) - 4(x + 1)
⇔ 2x + 14 + 24 = 15x - 3 - 4x - 4
⇔ 2x + 14 + 24 - 15x + 3 + 4x + 4 = 0
⇔ 45 - 9x = 0
⇔ 9(5 - x) = 0
⇔ 5 - x = 0
⇔ x = 5
Vậy: .......
d) 3(2x - 1) - 2(3 - x) = -1
⇔ 6x - 3 - 6 + 2x = -1
⇔ 6x - 3 - 6 + 2x + 1 = 0
⇔ 8x - 8 = 0
⇔ 8x = 8
⇔ x = 1
Vậy: ......
c) 2(x + 7) + 24 = 3(5x - 1) - 4(x + 1)
⇔ 2x + 14 + 24 = 15x - 3 - 4x - 4
⇔ 2x + 14 + 24 - 15x + 3 + 4x + 4 = 0
⇔ 45 - 9x = 0
⇔ 9(5 - x) = 0
⇔ 5 - x = 0
⇔ x = 5
Vậy: .......
d) 3(2x - 1) - 2(3 - x) = -1
⇔ 6x - 3 - 6 + 2x = -1
⇔ 6x - 3 - 6 + 2x + 1 = 0
⇔ 8x - 8 = 0
⇔ 8x = 8
⇔ x = 1
Vậy: ......