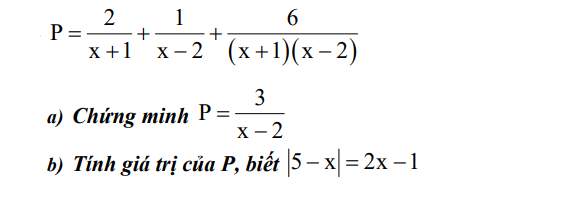b. th1: 5-x=2x-1 nếu 5-x>0 => x< 5
5-x=2x-1
-x-2x=-1-5
-3x= -6
x= 2 (chọn)
th2: 5-x=-2x-1 nếu 5-x<0 => x>5
5-x=-2x-1
-x+2x= -1-5
x= -6 (loại)
S={2}
Vậy giá trị của P là:
2.2-1= 3
a. <=> \(\dfrac{2.\left(x-2\right)}{\left(x+1\right)\left(x-2\right)}\)+\(\dfrac{x+1}{\left(x+1\right)\left(x-2\right)}\)+\(\dfrac{6}{\left(x+1\right)\left(x-2\right)}\)= \(\dfrac{3}{x-2}\)
<=> \(\dfrac{2.\left(x-2\right)}{\left(x+1\right)\left(x-2\right)}\)+\(\dfrac{x+1}{\left(x+1\right)\left(x-2\right)}\)+ \(\dfrac{6}{\left(x+1\right)\left(x-2\right)}\)= \(\dfrac{3.\left(x+1\right)}{\left(x+1\right)\left(x-2\right)}\)
<=> 2.(x-2) + x + 1 + 6= 3x + 3
<=> 2x - 4 + x + 1 +6 - 3x - 3= 0
<=> 0x =0
<=> x=0
Vậy P= \(\dfrac{3}{x-2}\)