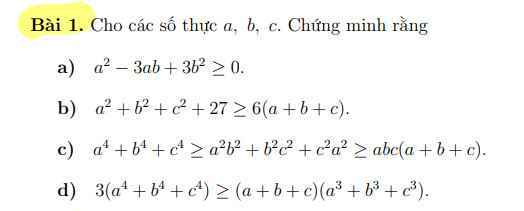a)\(a^2-3ab+3b^2\ge0\)
\(\Leftrightarrow a^2-2.\dfrac{3}{2}b+\dfrac{9}{4}b^2+\dfrac{3}{4}b^2\ge0\)
\(\Leftrightarrow\left(a-\dfrac{3}{2}b\right)^2+\dfrac{3}{4}b^2\ge0\) (luôn đúng).
b)\(a^2+b^2+c^2+27\)
\(=a^2+9+b^2+9+c^2+9\)
\(\ge6a+6b+6c=6\left(a+b+c\right)\)
c) \(a^4+b^4+c^4\ge a^2b^2+b^2c^2+c^2a^2\)
\(\Leftrightarrow a^4+b^4+c^4-a^2b^2-b^2c^2-c^2a^2\ge0\)
\(\Leftrightarrow2a^4+2b^4+c^4-2a^2b^2-2b^2c^2-2c^2a^2\ge0\)
\(\Leftrightarrow\left(a^2-b^2\right)^2+\left(b^2-c^2\right)^2+\left(c^2-a^2\right)^2\ge0\) (luôn đúng) (1)
\(a^2b^2+b^2c^2+c^2a^2\ge abc\left(a+b+c\right)\)
\(\Leftrightarrow a^2b^2+b^2c^2+c^2a^2-a^2bc-ab^2c-abc^2\ge0\)
\(\Leftrightarrow2a^2b^2+2b^2c^2+2c^2a^2-2a^2bc-2ab^2c-2abc^2\ge0\)
\(\Leftrightarrow\left(ab-bc\right)^2+\left(bc-ca\right)^2+\left(ca-ab\right)^2\ge0\) (luôn đúng) (2)
-Từ (1), (2) ta có điều cần phải c/m.