a: Khi m=0 thì pt sẽ là \(x^2-\left(2\cdot0+1\right)x+0^2+0-6=0\)
\(\Leftrightarrow x^2-x-6=0\)
=>x=3 hoặc x=-2
b: \(\text{Δ}=\left(2m+1\right)^2-4\left(m^2+m-6\right)\)
\(=4m^2+4m+1-4m^2-4m+24=25>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
cho pt:x2-2(m+1)x+4m=0
a) giải pt khi m=-2
b)tìm m để pt có 2 ngiệm x1,x2 thỏa mãn (x1+3)(x2+3)=3m2+12
Cho phương trình x2 - mx + 2m - 4 = 0. Tìm m để phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn |x1| + |x2| = 3
Cho m2 - (m+4)x + 3m +3 = 0.Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn x13 + x13 \(\ge\) 0
Cho phương trình bậc hai ẩn x sau:
x2 - 5x + 4 = 0
a) Chứng minh pt có hai nghiệm x1,x2
b) Tìm u,v biết u = x1 + x2, v = x1.x2
c) Lập phương trình bậc 2 có hai nghiệm là u,v
Cho phương trình: \(x^2-\left(2m+1\right)x-2m-2=0\)
Tìm giá trị m thỏa mãn \(x_1^3+x_2^3=26\)
Trong mặt phẳng toạ độ Oxy, cho (P) : y = x2 và (d) : y = -2m + m2 + 2 (m ≠ 0)
a, C/m với mọi giá trị m khác 0, (d) luôn cắt (P) tại 2 điểm phân biệt có hoành độ x1, x2 nằm về 2 phía của trục tung.
b, Tìm tất cả giá trị m ≠ 0 để √m - x1 . √m - x2 = 0
Giúp mik với !!!!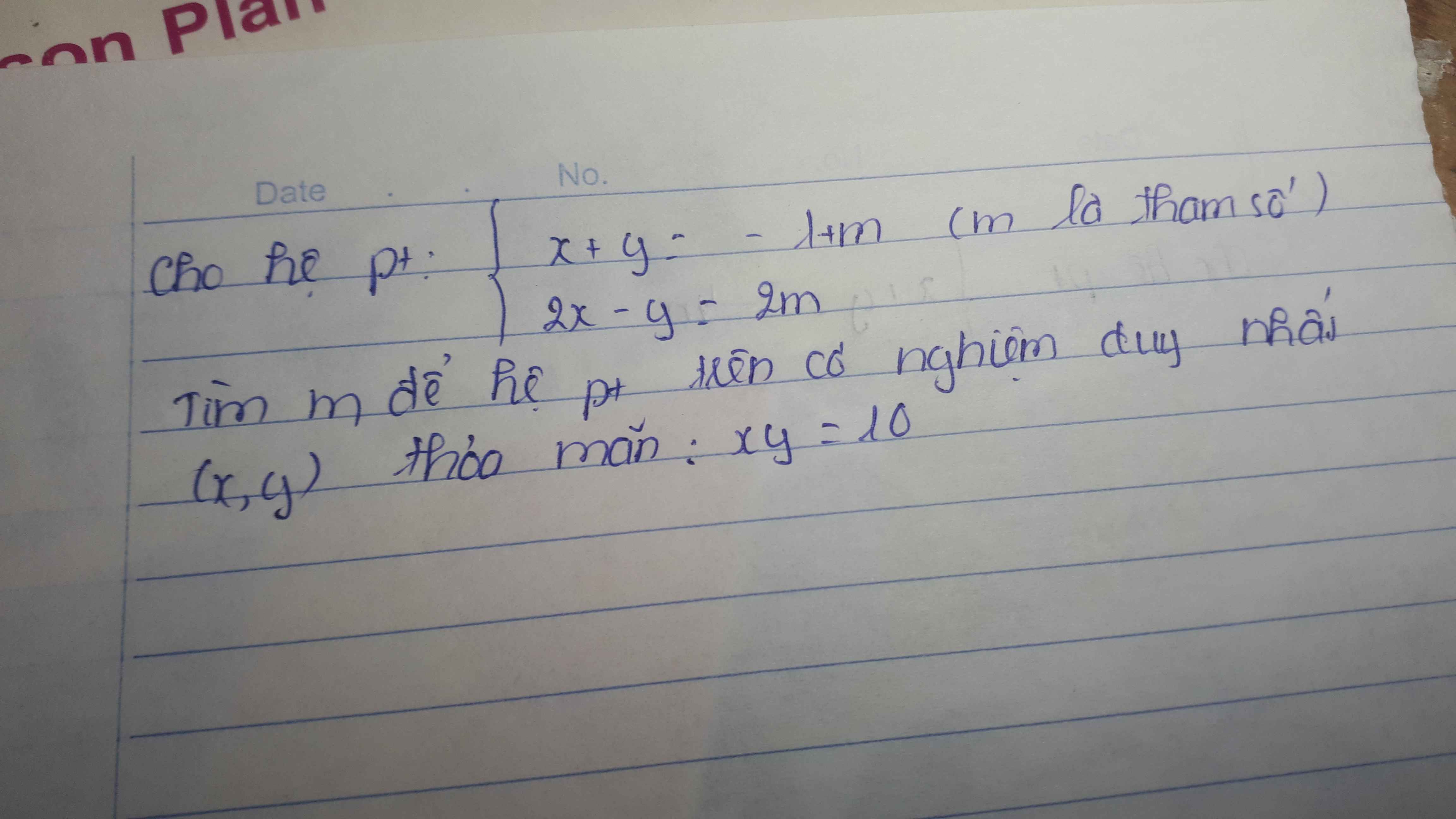
Giúp mik với !!!!
giải giùm nhé !
( -m - 1 )^2 - 1-3-m
