Question

Answer 1

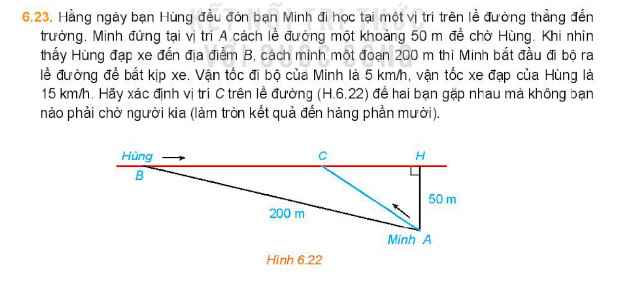
Do thời gian 2 người tới C bằng nhau nên: \(\dfrac{BC}{15}=\dfrac{AC}{5}\Rightarrow BC=3AC\)

Pitago: \(AC^2=AH^2+CH^2\Leftrightarrow\dfrac{BC^2}{9}=2500+CH^2\) (1)

\(BH=\sqrt{AB^2-AH^2}=50\sqrt{15}\)

\(\Rightarrow BC+CH=50\sqrt{15}\Rightarrow CH=50\sqrt{15}-BC\)

Thế vào (1):

\(\dfrac{1}{9}BC^2=2500+\left(50\sqrt{15}-BC\right)^2\)

\(\Rightarrow\dfrac{8}{9}BC^2-100\sqrt{15}BC+40000=0\Rightarrow\left[{}\begin{matrix}BC=267,5\left(m\right)>BH\left(loại\right)\\BC=168,2\left(m\right)\end{matrix}\right.\)

Vậy điểm C cách điểm B một đoạn 168,2 (m)