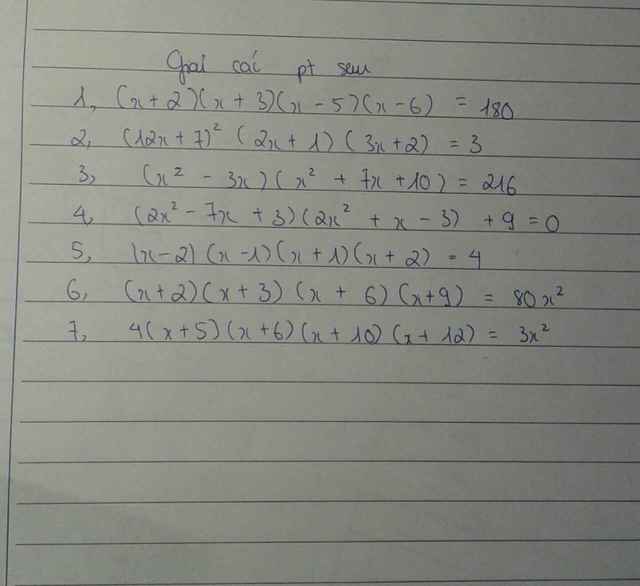\(\left(x+2\right)\left(x+3\right)\left(x-5\right)\left(x-6\right)=180.\\ \Leftrightarrow\left(x+2\right)\left(x-5\right)\left(x+3\right)\left(x-6\right)=180.\\ \Leftrightarrow\left(x^2-3x-10\right)\left(x^2-3x-18\right)=180.\\ \Leftrightarrow\left(x^2-3x-14+4\right)\left(x^2-3x-14-4\right)=180.\)
Đặt \(t=x^2-3x-14.\)
\(\Rightarrow\left(t+4\right)\left(t-4\right)=180.\\ \Leftrightarrow t^2-16=180.\\ \Leftrightarrow t^2=196.\)
\(\Leftrightarrow\left[{}\begin{matrix}t^2=14^2.\\t^2=\left(-14\right)^2.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=14.\\t=-14.\end{matrix}\right.\)
\(TH1:t=14.\\ \Rightarrow x^2-3x-14=14.\\ \Leftrightarrow x^2-3x-28=0.\\ \Leftrightarrow\left(x-7\right)\left(x+4\right)=0.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-7=0.\\x+4=0.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=7.\\x=-4.\end{matrix}\right.\)
\(TH2:t=-14.\\ \Rightarrow x^2-3x-14=-14.\\ \Leftrightarrow x^2-3x=0.\\ \Leftrightarrow x\left(x-3\right)=0.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0.\\x-3=0.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0.\\x=3.\end{matrix}\right.\)
Vậy phương trình có tập nghiệm là \(S=\left\{-4;0;3;7\right\}.\)