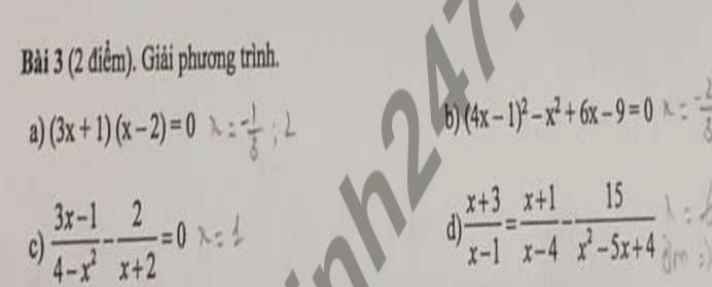Anh thấy em ghi đáp án bên cạnh rồi, em hỏi để xem cách làm hay dò kết quả đúng không nè?
a, \(\left(3x+1\right)\left(x-2\right)=0\Leftrightarrow x=-\dfrac{1}{3};x=2\)
b, \(\Leftrightarrow\left(4x-1\right)^2-\left(x^2-6x+9\right)=0\)
\(\Leftrightarrow\left(4x-1\right)^2-\left(x-3\right)^2=0\Leftrightarrow\left(3x+2\right)\left(5x-4\right)=0\Leftrightarrow x=-\dfrac{2}{3};x=\dfrac{5}{4}\)
c, đk : x khác 2 ; -2
\(\Rightarrow3x-1-2\left(2-x\right)=0\Leftrightarrow5x-5=0\Leftrightarrow x=1\)(tm)
d, đk x khác 1 ; 4
\(\Rightarrow\left(x+3\right)\left(x-4\right)=\left(x+1\right)\left(x-1\right)-15\)
\(\Leftrightarrow x^2-x-12=x^2-1-15\Leftrightarrow-x-12=-16\Leftrightarrow x=4\)(ktm)
vậy pt vô nghiệm
\(a,\\ \left(3x+1\right).\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}3x+1=0\\x-2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}3x=-1\\x=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=2\end{matrix}\right.\\ \Rightarrow S=\left\{-\dfrac{1}{3};2\right\}\\ b,\left(4x-1\right)^2-x^2+6x-9=0\\ \Leftrightarrow\left(4x-1\right)^2-\left(x^2-6x+9\right)=0\\ \Leftrightarrow\left(4x-1\right)^2-\left(x-3\right)^2=0\\ \Leftrightarrow\left[\left(4x-1\right)+\left(x-3\right)\right].\left[\left(4x-1\right)-\left(x-3\right)\right]=0\\ \Leftrightarrow\left(5x-4\right).\left(3x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}5x-4=0\\3x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}5x=4\\3x=-2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{5}\\x=-\dfrac{2}{3}\end{matrix}\right.\\ \Rightarrow S=\left\{-\dfrac{2}{3};\dfrac{4}{5}\right\}\)
\(c,ĐKXĐ:x\ne\pm2\\ \dfrac{3x-1}{4-x^2}-\dfrac{2}{x+2}=0\\ \Leftrightarrow\dfrac{1-3x}{x^2-4}-\dfrac{2\left(x-2\right)}{x^2-4}=0\\ \Leftrightarrow1-3x-2x+4=0\\ \Leftrightarrow-5x=-5\\ \Leftrightarrow x=\dfrac{-5}{-5}=1\left(TM\right)\\ \Rightarrow S=\left\{1\right\}\\ d,ĐKXĐ:x\ne1;x\ne4\\ \dfrac{x+3}{x-1}=\dfrac{x+1}{x-4}-\dfrac{15}{x^2-5x+4}\\ \Leftrightarrow\dfrac{\left(x+3\right).\left(x-4\right)}{x^2-5x+4}=\dfrac{\left(x+1\right).\left(x-1\right)-15}{x^2-5x+4}\\ \Leftrightarrow x^2+3x-4x-12=x^2-1-15\\ \Leftrightarrow x^2-x^2+3x-4x=-1-15+12\\ \Leftrightarrow-x=-4\\ \Leftrightarrow x=\dfrac{-4}{-1}=4\left(KTM\right)\\ \Rightarrow S=\varnothing\)
Đây là cách làm em nha!