Question

Answer 1

giải cho mik câu 28 và câu 29 nhé 

Answer 2

???????????????????

 

Answer 3

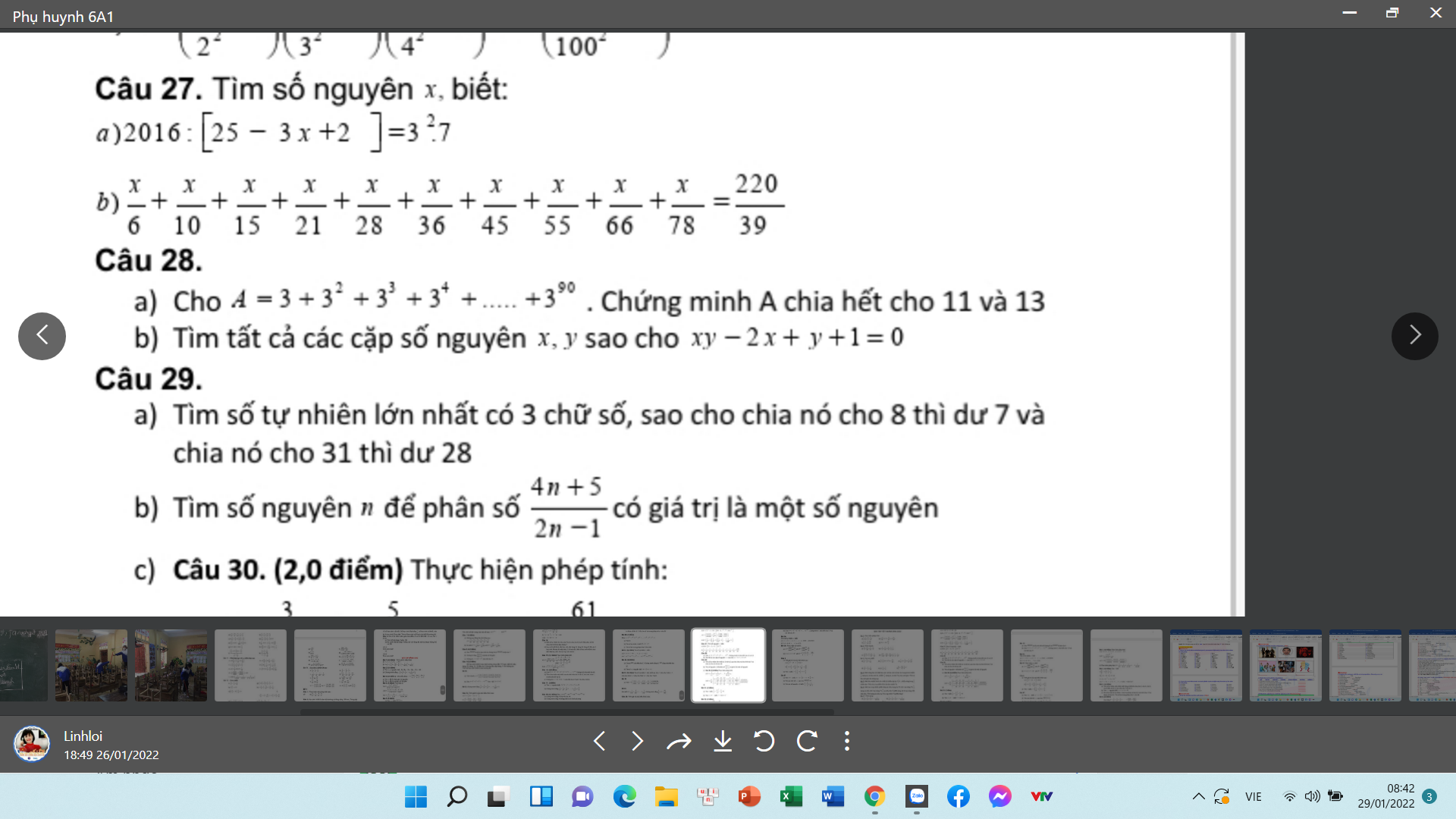
Câu 28:

\(a,A=3+3^2+3^3+3^4+...+3^{90}\\ =3.\left(1+3+3^2\right)+3^4.\left(1+3+3^2\right)+...+3^{88}.\left(1+3+3^2\right)\\ =\left(3+3^4+3^7+...+3^{85}+3^{88}\right).13⋮13\\ A=3+3^2+3^3+3^4+...+3^{89}+3^{90}=3.\left(1+3+3^2+3^3+3^4\right)+...+3^{86}.\left(1+3+3^2+3^3+3^4\right)\\ =121.\left(3+3^6+3^{11}+...+3^{86}\right)⋮11\\ \)

=> A vừa chia hết cho 11 vừa chia hết cho 13

Answer 4

29 

a,tk

Answer 5

Câu 28:

b) xy-2x+y+1=0 =>y(x+1)=2x-1

=>y=\(\dfrac{2x-1}{x+1}\). (x≠-1) .Vì y là số nguyên nên:

2x-1 ⋮ x+1

=>2(x+1)-3 ⋮ x+1

=>3 ⋮ x+1

=>x+1∈Ư(3)

=>x+1∈{1;-1;3;-3}

=>x∈{0;-2;2;-4}

=>y∈{-1;5;1;-3}

- Vậy các cặp số (x,y) là (0;-1) , (-2;5) , (2;1) , (-4;-3).

Answer 6

Câu 29:

b) - Để phân số \(\dfrac{4n+5}{2n-1}\) có giá tri là 1 số nguyên thì:

4n+5 ⋮ 2n-1

=>2(2n-1)+7 ⋮ 2n-1

=>7⋮ 2n-1

=>2n-1∈Ư(7)

\(\begin{matrix}2n-1&1&7&-1&-7\\n&1&4&0&-3\end{matrix}\)