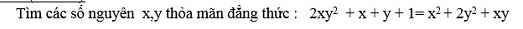Question

Answer 1

Ta thấy \(x=1\) không phải nghiệm PT

\(PT\Leftrightarrow2y^2\left(x-1\right)-x\left(x-1\right)-y\left(x-1\right)+1=0\)

Chia 2 vế cho \(x-1\)

\(PT\Leftrightarrow2y^2-x-y+\dfrac{1}{x-1}=0\)

Vì \(x,y\in Z\Leftrightarrow x-1\inƯ\left(1\right)=\left\{-1;1\right\}\Leftrightarrow x\in\left\{0;2\right\}\)

Với \(x=0\Leftrightarrow2y^2-y-1=0\Leftrightarrow\left[{}\begin{matrix}y=1\\y=-\dfrac{1}{2}\end{matrix}\right.\)

Với \(x=2\Leftrightarrow2y^2-y-1=0\Leftrightarrow\left[{}\begin{matrix}y=1\\y=-\dfrac{1}{2}\end{matrix}\right.\)

Vậy \(\left(x;y\right)=\left(0;1\right);\left(2;1\right)\)