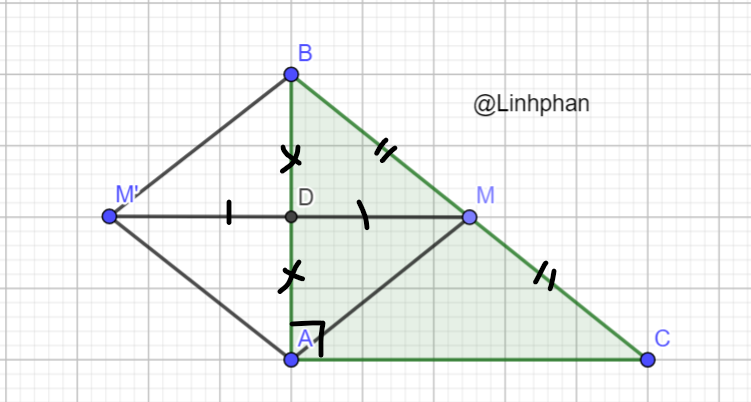
Vì D là trung điểm MM' và AB nên \(AMBM'\) là hbh
Lại có D,M là trung điểm AB,BC nên DM là đtb
Do đó \(DM//AC\)
Mà \(AC\bot AB\) nên \(MD\bot AB\) hay \(MM'\bot AB\)
Vậy \(AMBM'\) là hình thoi
Vì AM là đường trung tuyến => M là trung điểm của BC => BC = CM
Xét ΔABC có: D là trung điểm của AB (gt) ; M là trung điểm của BC (cmt)
=> DM là đường trung bình của ΔABC
=> DM // AC ( t/c đg tb) mà BA ⊥ AC ( do \(\hat{BAC} = 90^0\) )
=> DM ⊥ AB => \(\hat{ADM} = 90^0\)
+, Xét tứ giác AMBM' có:
D là trung điểm của AB (gt)
D là trung điểm của MM' (do M đối xứng với M' qua D)
mà AB cắt MM' tại D
=> Tứ gíac AMBM' la hình bình hành (dhnb)
mà \(\hat{ADM} = 90^0\)
=> Tứ giác AMBM' là hình thoi (dhnb)