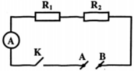
Câu 1:
\(R_{tđ}=R_1+R_2=15+9=24\left(\Omega\right)\)
\(I=I_1=I_2=\dfrac{U}{R_{tđ}}=\dfrac{21}{24}=0,875\left(A\right)\)
\(\left\{{}\begin{matrix}U_1=I_1.R_1=0,875.15=13,125\left(V\right)\\U_2=I_2.R_2=0,875.9=7,875\left(V\right)\end{matrix}\right.\)
\(\left\{{}\begin{matrix}P_{R_{tđ}}=U.I=21.0,875=18,375\left(W\right)\\P_1=U_1.I_1=13,125.0,875=\dfrac{735}{64}\left(W\right)\\P_2=U_2.I_2=7,875.0,875=\dfrac{441}{64}\left(W\right)\end{matrix}\right.\)
\(A=P.t=U.I.t=21.0,875.3.60=3307,5\left(J\right)\)
\(U_3=U_2=7,875\left(V\right)\)
\(I_3=\dfrac{U_3}{R_3}=\dfrac{7,875}{15}=0,525\left(A\right)\)
Câu 2:
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{30.20}{30+20}=12\left(\Omega\right)\)
\(U=U_1=U_2=24V\)
\(\left\{{}\begin{matrix}I=\dfrac{U}{R_{tđ}}=\dfrac{24}{12}=2\left(A\right)\\I_1=\dfrac{U_1}{R_1}=\dfrac{24}{30}=0,8\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{24}{20}=1,2\left(A\right)\end{matrix}\right.\)
\(\left\{{}\begin{matrix}P_m=U.I=24.2=48\left(W\right)\\P_1=U_1.I_1=24.0,8=19,2\left(W\right)\\P_2=U_2.I_2=24.1,2=28,8\left(W\right)\end{matrix}\right.\)
\(A=P.t=48.3.60=8640\left(J\right)\)
Câu 3:
\(R_{tđ}=R_1+R_2=15+10=25\left(\Omega\right)\)
\(I=I_1=I_2=\dfrac{U}{R_{tđ}}=\dfrac{4,5}{25}=0,18\left(A\right)\)