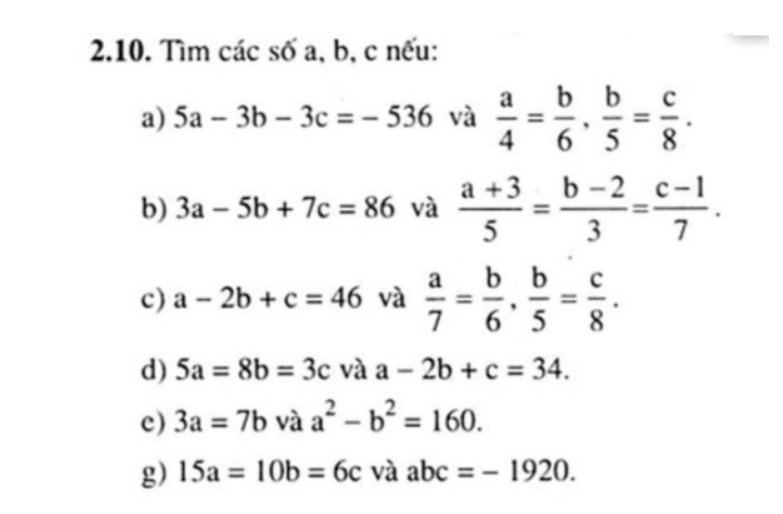a, \(\dfrac{a}{4}=\dfrac{b}{6};\dfrac{b}{5}=\dfrac{c}{8}\Rightarrow\dfrac{a}{20}=\dfrac{b}{30}=\dfrac{c}{48}\)
Áp dụng tcdtsbn:
\(\dfrac{a}{20}=\dfrac{b}{30}=\dfrac{c}{48}=\dfrac{5a-3b-3c}{100-90-144}=\dfrac{-536}{-134}=4\\ \Rightarrow\left\{{}\begin{matrix}a=80\\b=120\\c=192\end{matrix}\right.\)
b, Áp dụng tcdtsbn:
\(\dfrac{a+3}{5}=\dfrac{b-2}{3}=\dfrac{c-1}{7}=\dfrac{3a+9-5b+10+7c-7}{5\cdot3-3\cdot5+7\cdot7}=\dfrac{98}{49}=2\\ \Rightarrow\left\{{}\begin{matrix}a+3=10\\b-2=6\\c-1=14\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=7\\b=8\\c=15\end{matrix}\right.\)
\(c,\dfrac{a}{7}=\dfrac{b}{6};\dfrac{b}{5}=\dfrac{c}{8}\Rightarrow\dfrac{a}{35}=\dfrac{b}{30}=\dfrac{c}{48}\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{35}=\dfrac{b}{40}=\dfrac{c}{48}=\dfrac{a-2b+c}{35-80+48}=\dfrac{46}{3}\\ \Rightarrow\left\{{}\begin{matrix}a=\dfrac{1610}{3}\\b=\dfrac{1840}{3}\\c=736\end{matrix}\right.\)
\(d,5a=8b=3c\Rightarrow\dfrac{a}{\dfrac{1}{5}}=\dfrac{b}{\dfrac{1}{8}}=\dfrac{c}{\dfrac{1}{3}}\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{\dfrac{1}{5}}=\dfrac{b}{\dfrac{1}{8}}=\dfrac{c}{\dfrac{1}{3}}=\dfrac{a-2b+c}{\dfrac{1}{5}-\dfrac{1}{4}+\dfrac{1}{3}}=\dfrac{34}{\dfrac{17}{60}}=120\\ \Rightarrow\left\{{}\begin{matrix}a=24\\b=15\\c=40\end{matrix}\right.\)
\(e,3a=7b\Rightarrow\dfrac{a}{7}=\dfrac{b}{3}\)
Đặt \(\dfrac{a}{7}=\dfrac{b}{3}=k\Rightarrow a=7k;b=3k\)
\(a^2-b^2=160\\ \Rightarrow49k^2-9k^2=160\\ \Rightarrow k^2=4\Rightarrow\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=14;y=6\\x=-14;y=-6\end{matrix}\right.\)
\(g,15a=10b=6c\Rightarrow\dfrac{15a}{30}=\dfrac{10b}{30}=\dfrac{6c}{30}\Rightarrow\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{5}\)
Đặt \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{5}=k\Rightarrow a=2k;b=3k;c=5k\)
\(abc=-1920\\ \Rightarrow30k^3=-1920\\ \Rightarrow k^3=-64=\left(-4\right)^3\\ \Rightarrow k=-4\\ \Rightarrow\left\{{}\begin{matrix}a=-8\\b=-12\\c=-20\end{matrix}\right.\)