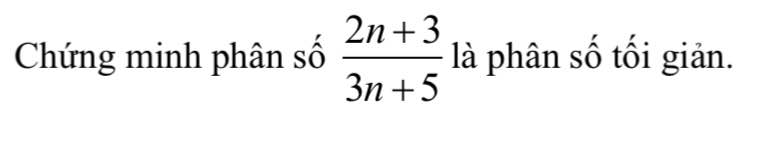Question

 

Answer 1

Gọi \(d=ƯCLN\left(2n+3,3n+5\right)\)

\(\Rightarrow\left\{{}\begin{matrix}2n+3⋮d\\3n+5⋮d\end{matrix}\right.\Rightarrow3\left(2n+3\right)-2\left(3n+5\right)⋮d\\ \Rightarrow6n+9-6n-10⋮d\\ \Rightarrow-1⋮d\\ \Rightarrow d=1\)

Do đó 2n+3 và 3n+5 ntcn

Vậy p/số \(\dfrac{2n+3}{3n+5}\) tối giản

Answer 2

Gọi d là ƯC(2n+3,3n+5)

⇒\(\left\{{}\begin{matrix}2n+3\text{⋮d}\\3n+5\text{⋮}d\end{matrix}\right.\)

⇒\(\left\{{}\begin{matrix}6n+9\text{⋮}d\\6n+10\text{⋮}d\end{matrix}\right.\)

⇒ \(\left(6n+10\right)-\left(6n+9\right)\text{⋮}d\)

⇒ \(1\text{⋮}d\)

⇒ \(d=1\)

Vậy ...