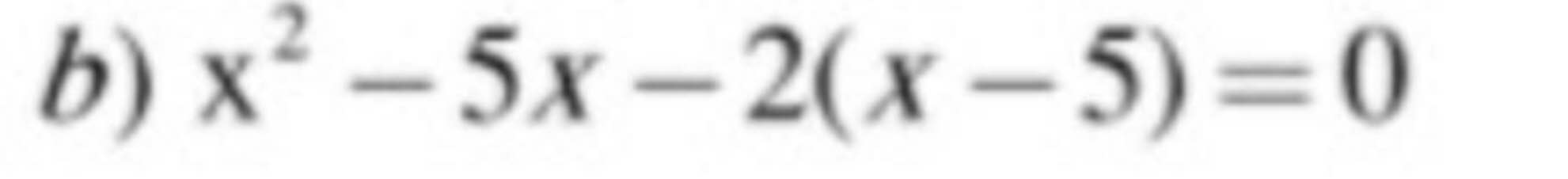Question

Answer 1

\(b)x^2-5x-2(x-5)=0\\<=>(x^2-5x)-2(x-5)=0\\<=>x(x-5)-2(x-5)=0\\<=>(x-5)(x-2)=0\\\)

\(< =>\left[{}\begin{matrix}x-5=0\\x-2=0\end{matrix}\right.< =>\left[{}\begin{matrix}x=5\\x=2\end{matrix}\right.\)

Vậy x =5 hoặc x =2

Answer 2

\(x^2-5x-2\left(x-5\right)=0\)

\(\Rightarrow x\left(x-5\right)-2\left(x-5\right)=0\)

\(\Rightarrow\left(x-5\right)\left(x-2\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=5\\x=2\end{matrix}\right.\)