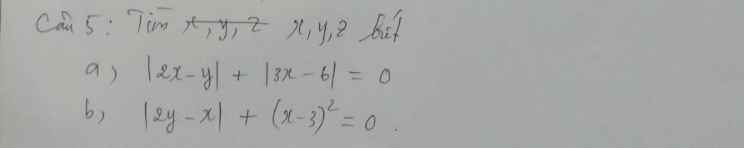\(a,\Leftrightarrow\left\{{}\begin{matrix}2x-y=0\\3x-6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=y\\x=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=4\end{matrix}\right.\\ b,\Leftrightarrow\left\{{}\begin{matrix}2y-x=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\2y=x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=\dfrac{3}{2}\end{matrix}\right.\)
a/ $\begin{cases}|2x-y|\ge 0\\|3x-6|\ge 0\end{cases}$
$\Rightarrow |2x-y|+|3x-6|\ge 0$
Dấu "=" xảy ra khi $2x-y=3x-6=0$
$\Leftrightarrow x=2;y=6$
b/ $\begin{cases}|2y-x|\ge 0\\(x-3)^2\ge 0\end{cases}$
$\Rightarrow |2y-x|+(x-3)^2\ge 0$
Dấu "=" xảy ra khi $2y-x=x-3=0$
$\Leftrightarrow x=3;y=1;5$