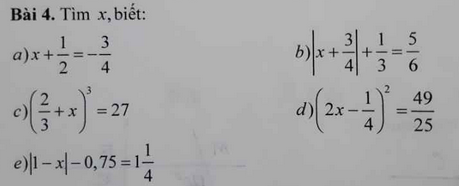\(a,\Rightarrow x=-\dfrac{5}{4}\\ b,\Rightarrow\left|x+\dfrac{3}{4}\right|=\dfrac{1}{2}\\ \Rightarrow\left[{}\begin{matrix}x+\dfrac{3}{4}=\dfrac{1}{2}\left(x\ge-\dfrac{3}{4}\right)\\x+\dfrac{3}{4}=-\dfrac{1}{2}\left(x< -\dfrac{3}{4}\right)\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{4}\left(tm\right)\\x=-\dfrac{5}{4}\left(tm\right)\end{matrix}\right.\\ c,\Rightarrow\dfrac{2}{3}+x=3\Rightarrow x=\dfrac{7}{3}\\ d,\Rightarrow\left[{}\begin{matrix}2x-\dfrac{1}{4}=\dfrac{7}{5}\\2x-\dfrac{1}{4}=-\dfrac{7}{5}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2x=\dfrac{33}{20}\\2x=-\dfrac{23}{20}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{33}{40}\\x=-\dfrac{23}{40}\end{matrix}\right.\)
\(e,\Rightarrow\left|1-x\right|=\dfrac{5}{4}+\dfrac{3}{4}=2\\ \Rightarrow\left[{}\begin{matrix}1-x=2\left(x\le1\right)\\x-1=2\left(x>1\right)\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-1\left(tm\right)\\x=3\left(tm\right)\end{matrix}\right.\)