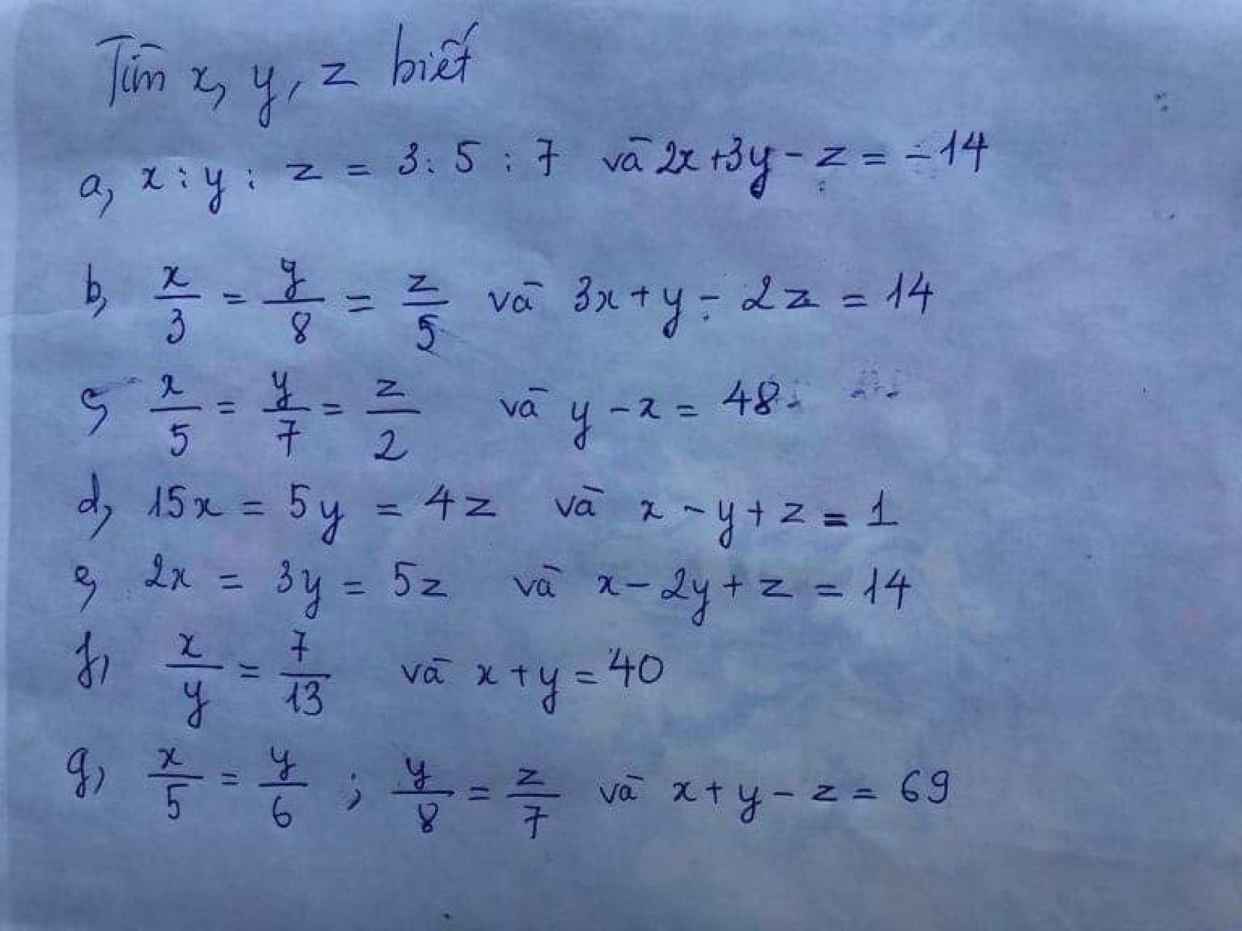\(a,x:y:z=3:5:7\Rightarrow\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{2x}{6}=\dfrac{3y}{15}=\dfrac{2x+3y-z}{6+15-7}=\dfrac{-14}{14}=-1\\ \Rightarrow\left\{{}\begin{matrix}x=-3\\y=-5\\z=-7\end{matrix}\right.\)
\(b,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{3}=\dfrac{y}{8}=\dfrac{z}{5}=\dfrac{3x}{9}=\dfrac{2z}{10}=\dfrac{3x+y-2z}{9+8-10}=\dfrac{14}{7}=2\\ \Rightarrow\left\{{}\begin{matrix}x=6\\y=16\\z=10\end{matrix}\right.\)
\(c,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{5}=\dfrac{y}{7}=\dfrac{z}{2}=\dfrac{y-x}{7-5}=\dfrac{48}{2}=24\\ \Rightarrow\left\{{}\begin{matrix}x=120\\y=168\\z=48\end{matrix}\right.\)
\(d,15x=5y=4z\Rightarrow\dfrac{x}{\dfrac{1}{15}}=\dfrac{y}{\dfrac{1}{5}}=\dfrac{z}{\dfrac{1}{4}}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{\dfrac{1}{15}}=\dfrac{y}{\dfrac{1}{5}}=\dfrac{z}{\dfrac{1}{4}}=\dfrac{x-y+z}{\dfrac{1}{15}-\dfrac{1}{5}+\dfrac{1}{4}}=\dfrac{1}{\dfrac{7}{60}}=\dfrac{60}{7}\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{60}{7}\cdot\dfrac{1}{15}=\dfrac{4}{7}\\y=\dfrac{60}{7}\cdot\dfrac{1}{5}=\dfrac{12}{7}\\z=\dfrac{60}{7}\cdot\dfrac{1}{4}=\dfrac{15}{7}\end{matrix}\right.\)
\(e,2x=3y=5z\Rightarrow\dfrac{2x}{30}=\dfrac{3y}{30}=\dfrac{5z}{30}\Rightarrow\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{2y}{20}=\dfrac{x-2y+z}{15-20+6}=\dfrac{15}{1}=15\\ \Rightarrow\left\{{}\begin{matrix}x=15\\y=10\\z=6\end{matrix}\right.\)
\(f,\dfrac{x}{y}=\dfrac{7}{13}\Rightarrow\dfrac{x}{7}=\dfrac{y}{13}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{7}=\dfrac{y}{13}=\dfrac{x+y}{7+13}=\dfrac{40}{20}=2\\ \Rightarrow\left\{{}\begin{matrix}x=14\\y=26\end{matrix}\right.\)
\(g,\dfrac{x}{5}=\dfrac{y}{6}\Rightarrow\dfrac{x}{20}=\dfrac{y}{24};\dfrac{y}{8}=\dfrac{z}{7}\Rightarrow\dfrac{y}{24}=\dfrac{z}{21}\\ \Rightarrow\dfrac{x}{20}=\dfrac{y}{24}=\dfrac{z}{21}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{20}=\dfrac{y}{24}=\dfrac{z}{21}=\dfrac{x+y-z}{20+24-21}=\dfrac{69}{23}=3\\ \Rightarrow\left\{{}\begin{matrix}x=60\\y=72\\z=63\end{matrix}\right.\)