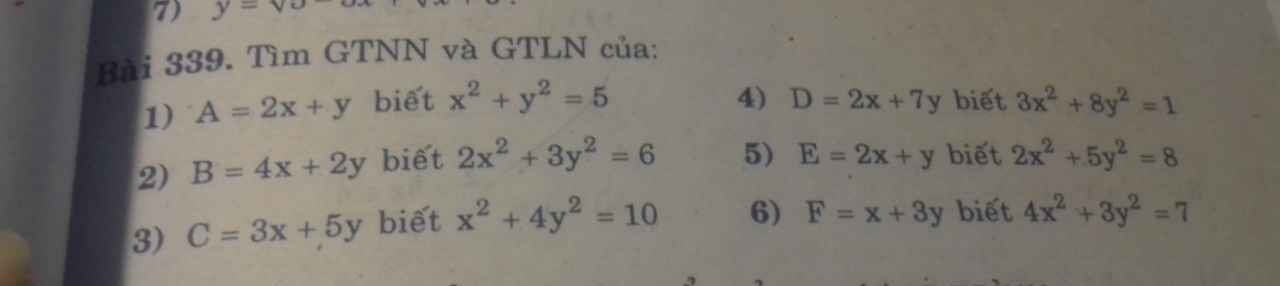Question

Answer 1

1. Áp dụng BĐT Bunhiacopkxy:

$A^2=(2x+y)^2\leq (x^2+y^2)(2^2+1^2)=5.5=25$

$\Rightarrow -5\leq A\leq 5$

Vậy $A_{\max}=5; A_{\min}=-5$

2. Áp dụng BĐT Bunhiacopxky:
$B^2=(4x+2y)^2\leq (2x^2+3y^2)(8+\frac{4}{3})=6.\frac{28}{3}=56$

$\Rightarrow -2\sqrt{14}\leq B\leq 2\sqrt{14}$

Vậy $B_{\min}=-2\sqrt{14}$ khi $(x,y)=(-3\sqrt{\frac{2}{7}}, -\sqrt{\frac{2}{7}})$

$B_{\max}=2\sqrt{14}$ khi $(x,y)=(3\sqrt{\frac{2}{7}}, \sqrt{\frac{2}{7}})$

Answer 2

3. 

Áp dụng BĐT Bunhiacopxky:

$C^2=(3x+5y)^2\leq (x^2+4y^2)(3^2+\frac{25}{4})=10.\frac{61}{4}=\frac{305}{2}$

$\Rightarrow -\sqrt{\frac{305}{2}}\leq C\leq \sqrt{\frac{305}{2}}$

Vậy:

$C_{\min}=-\sqrt{\frac{305}{2}}$ khi $(x,y)=(-6\sqrt{\frac{10}{61}},-5\sqrt{\frac{5}{122}})$

$C_{\max}=\sqrt{\frac{305}{2}}$ khi $(x,y)=(6\sqrt{\frac{10}{61}},5\sqrt{\frac{5}{122}})$

 

Answer 3

5.

Áp dụng BĐT Bunhiacopxky:

$E^2=(2x+y)^2\leq (2x^2+5y^2)(2+\frac{1}{5})=8.\frac{11}{5}=\frac{88}{5}$

$\Rightarrow -2\sqrt{\frac{22}{5}}\leq E\leq 2\sqrt{\frac{22}{5}}$

Vậy:

$E_{\min}=-2\sqrt{\frac{22}{5}}$ khi $(x,y)=(-2\sqrt{\frac{10}{11}}, -2\sqrt{\frac{2}{5}})$

$E_{\max}=2\sqrt{\frac{22}{5}}$ khi $(x,y)=(2\sqrt{\frac{10}{11}}, 2\sqrt{\frac{2}{5}})$

Answer 4

4. Áp dụng BĐT Bunhiacopxky:
$D^2=(2x+7y)^2\leq (3x^2+8y^2)(\frac{4}{3}+\frac{49}{8})=\frac{179}{24}$

$\Rightarrow -\sqrt{\frac{179}{24}}\leq D\leq \sqrt{\frac{179}{24}}$

Vậy:

$D_{\min}=-\sqrt{\frac{179}{24}}$ khi \((x,y)=(-\sqrt{\frac{32}{537}}, -\sqrt{\frac{147}{1432}})\)

$D_{\max}=\sqrt{\frac{179}{24}}$ khi $(x,y)=(\sqrt{\frac{32}{537}}, \sqrt{\frac{147}{1432}})$