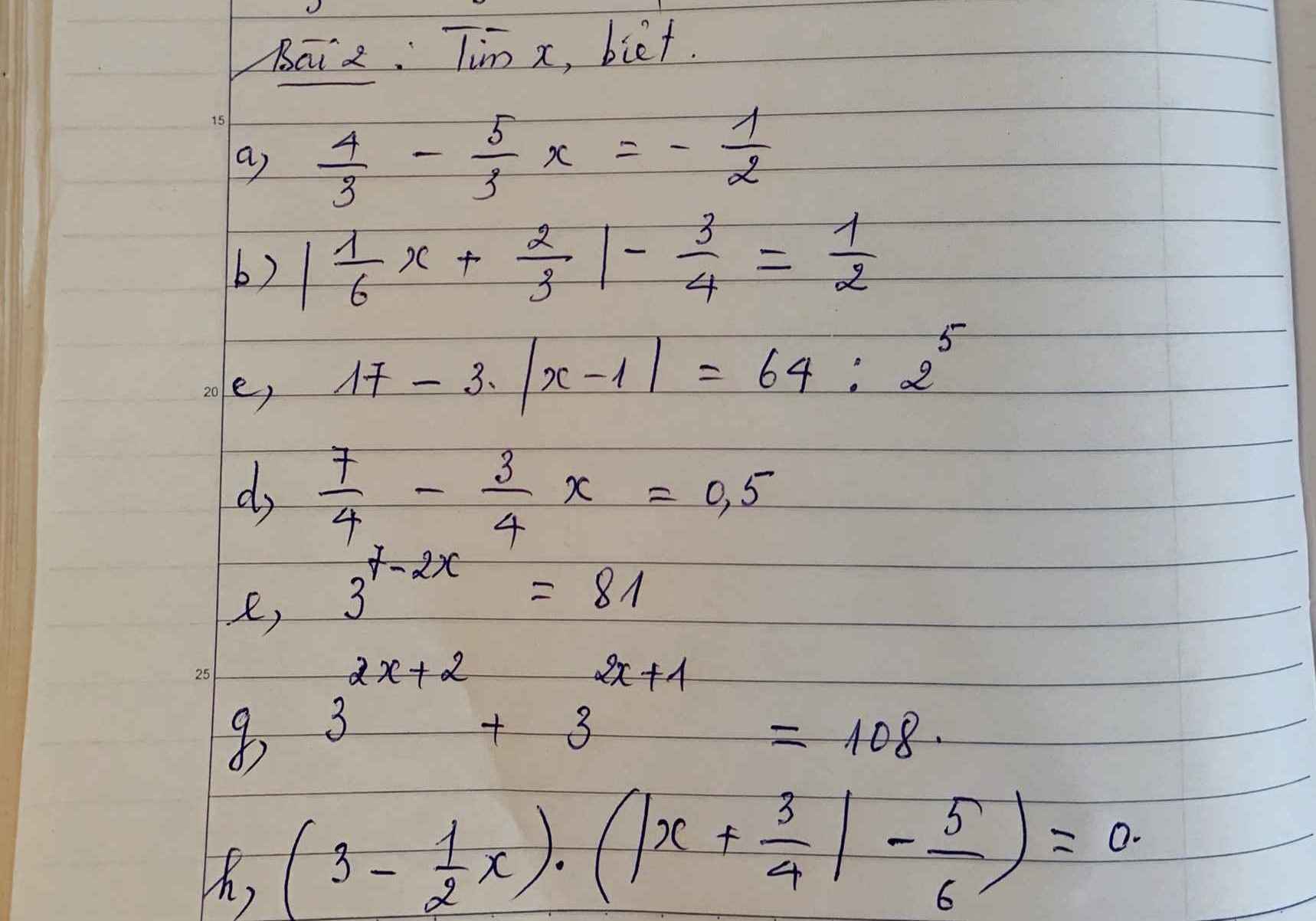\(a,\Rightarrow-\dfrac{5}{3}x=-\dfrac{1}{2}-\dfrac{4}{3}=-\dfrac{11}{6}\Rightarrow x=-\dfrac{11}{6}\cdot\left(-\dfrac{3}{5}\right)=\dfrac{11}{10}\\ b,\Rightarrow\left|\dfrac{1}{6}x+\dfrac{2}{3}\right|=\dfrac{5}{4}\\ \Rightarrow\left[{}\begin{matrix}\dfrac{1}{6}x+\dfrac{2}{3}=\dfrac{5}{4}\\\dfrac{1}{6}x+\dfrac{2}{3}=-\dfrac{5}{4}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\dfrac{1}{6}x=\dfrac{7}{12}\\\dfrac{1}{6}x=-\dfrac{23}{12}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-\dfrac{23}{2}\end{matrix}\right.\)
\(c,\Rightarrow3\left|x-1\right|=17-2^6:2^5\\ \Rightarrow3\left|x-1\right|=15\Rightarrow\left|x-1\right|=5\\ \Rightarrow\left[{}\begin{matrix}x-1=5\\x-1=-5\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=6\\x=-4\end{matrix}\right.\)
\(d,\Rightarrow-\dfrac{3}{4}x=\dfrac{1}{2}-\dfrac{7}{4}=-\dfrac{5}{4}\\ \Rightarrow x=\dfrac{5}{3}\\ e,3^{7-2x}=81=3^4\\ \Rightarrow7-2x=4\Rightarrow x=\dfrac{3}{2}\\ g,3^{2x+2}+3^{2x+1}=108\\ \Rightarrow3^{2x+1}\cdot4=108\Rightarrow3^{2x+1}=27=3^3\\ \Rightarrow2x+1=3\Rightarrow x=1\)
\(h,\Rightarrow\left[{}\begin{matrix}\dfrac{1}{2}x=3\\\left|x+\dfrac{3}{4}\right|=\dfrac{5}{6}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=6\\x+\dfrac{3}{4}=-\dfrac{5}{6}\\x+\dfrac{3}{4}=\dfrac{5}{6}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=6\\x=-\dfrac{19}{12}\\x=\dfrac{1}{12}\end{matrix}\right.\)