a,\(\Rightarrow\left\{{}\begin{matrix}R1=\dfrac{U1^2}{P1}=24\Omega\\R2=\dfrac{U2^2}{P2}=3\Omega\end{matrix}\right.\)\(\Rightarrow l\left(mn\right)=\dfrac{RS}{p}=\dfrac{2.0,4.10^{-6}}{0,2.10^{-6}}=4m\)
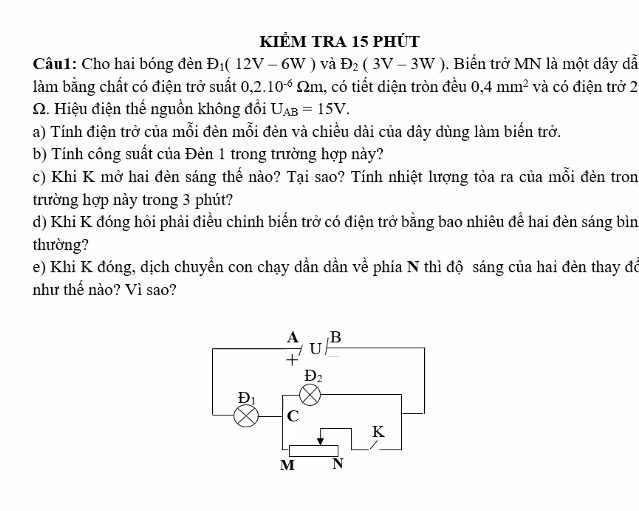
b. R1 nt( R2//Rmn)
\(\Rightarrow I1=\dfrac{15}{R1+\dfrac{R2Rmn}{R2+Rmn}}=0,6A\Rightarrow P1=I1^2R1=8,64w\)
c,=>R1 nt R2 \(\Rightarrow I1=I2=\dfrac{15}{R1+R2}=0,56A\Rightarrow\left\{{}\begin{matrix}I1>Idm1\\I2< Idm2\end{matrix}\right.\)
=>den 1 sang manh hon bth m den 2 sang yeu hon bth
\(\Rightarrow\left\{{}\begin{matrix}Q1=I1^2R1t=1354,752J\\Q2=I2^2R2t=169,344J\end{matrix}\right.\)
d, =>R1 nt(R2//Rmn)
\(\Rightarrow\left\{{}\begin{matrix}I1=Idm1=0,5A\\I2=Idm2=1A\end{matrix}\right.\)\(\Rightarrow\)\(\Rightarrow I2>I1???\) nen ko the dieu chinh MN de thoa man 2 den sang bth
e, dich chuyen con chay ve phia N\(\Rightarrow Rmn\uparrow\)
\(\Rightarrow\left\{{}\begin{matrix}I1=\dfrac{15}{24+\dfrac{3Rmn}{3+Rmn}}\left(A\right)\Rightarrow I1\downarrow\\I2=\dfrac{U2}{3}=\dfrac{15-U1}{3}\Rightarrow I2\uparrow\end{matrix}\right.\)