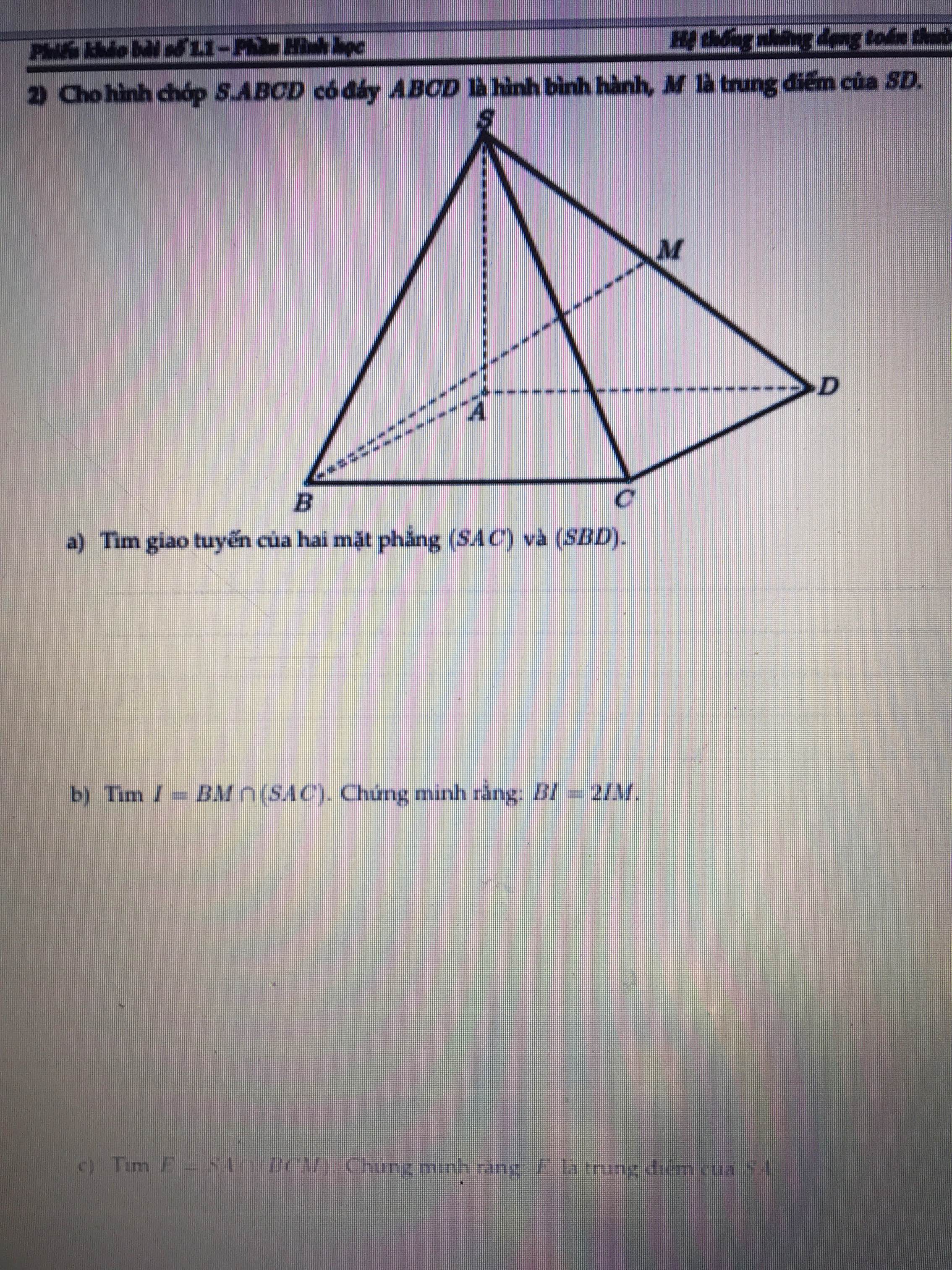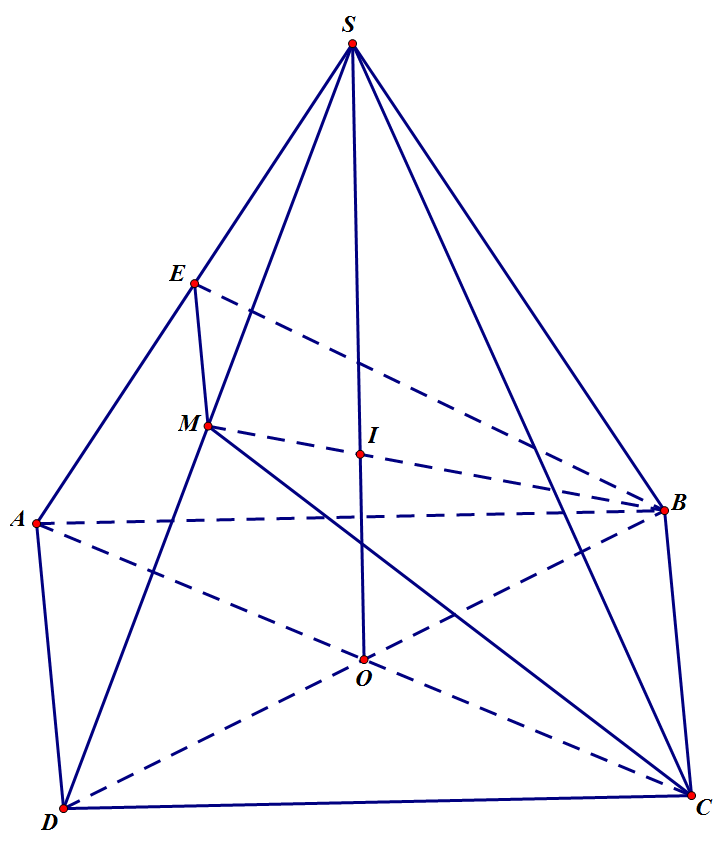
a, Trong mặt phẳng đáy (ABCD) gọi O là giao điểm của AC và BD
⇒ \(\left\{{}\begin{matrix}O\in\left(SAC\right)\\O\in\left(SBD\right)\end{matrix}\right.\). Mà \(\left\{{}\begin{matrix}S\in\left(SAC\right)\\S\in\left(SBD\right)\end{matrix}\right.\)
⇒ SO = (SAC) \(\cap\) (SBD)
b, I = BM \(\cap\left(SAC\right)\)
Mà BM \(\subset\) (SBD)
⇒ I ∈ (SBD)
⇒ I nằm trên giao tuyến của (SAC) và (SBD)
⇒ I ∈ SO
⇒ I là giao điểm của SO và AC trong (SAC)
Do tứ giác ABCD là hình bình hành có O là giao điểm của hai đường chéo AC và BD
⇒ O là trung điểm của AC và BD
ΔSBD có hai đường trung tuyến SO và BM cắt nhau tại I
⇒ I là trọng tâm của ΔSBD
Mà BM là đường trung tuyến của ΔSBD
⇒ BI = 2IM
c, E = SA \(\cap\) (BCM)
⇒ \(\left\{{}\begin{matrix}E\in\left(SAD\right)\\E\in\left(BCM\right)\end{matrix}\right.\)
⇒ E nằm trên giao tuyến của (SAD) và (BCM)
Mặt khác : (SAD) và (BCM) có chung điểm M. Mà AD nằm trong (SAD) ; BC nằm trong (BCM) và ta có AD//BC (hai cạnh đối của hình bình hành)
⇒ (SAD) \(\cap\) (BCM) = d. Với d là đường thẳng đi qua M và song song với AD
⇒ E là giao điểm của d với SA
ΔSAD có ME // AD. Mà M là trung điểm của SD
⇒ E là trung điểm của SA