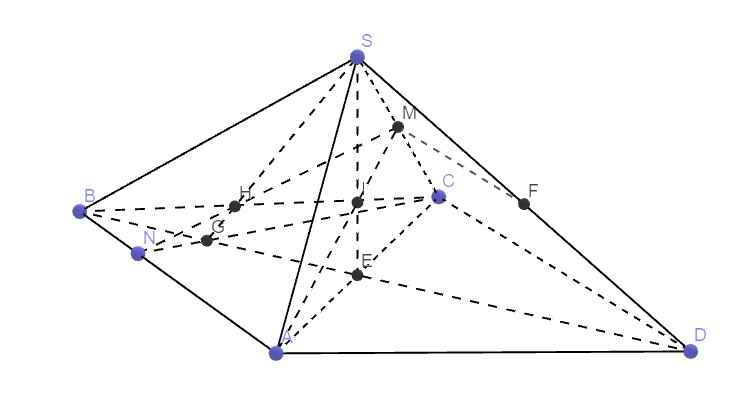
Gọi E là giao điểm AC và BD. Do ABCD là hình bình hành \(\Rightarrow\) E là trung điểm AC và BD
Trong mp (SAC), nối AM cắt SE tại I
\(\left\{{}\begin{matrix}I\in AM\\I\in SE\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow I=AM\cap\left(SBD\right)\)
Do E là trung điểm AC, M là trung điểm SC \(\Rightarrow\) I là trọng tâm tam giác SAC
\(\Rightarrow IA=2IM\) (tính chất trọng tâm)
b.
Trong mp (SCD), qua M kẻ đường thẳng song song CD cắt SD tại F
\(MF||CD\Rightarrow MF||AB\)
Mà \(M\in\left(ABM\right)\Rightarrow F\in\left(ABM\right)\)
\(\Rightarrow F=SD\cap\left(ABM\right)\)
Trong tam giác SCD, ta có M là trung điểm SC và \(MF||CD\Rightarrow MF\) là đường trung bình tam giác SCD
\(\Rightarrow\) F là trung điểm SD
c.
Trong mp (ABCD), nối CN cắt BD tại G \(\Rightarrow G\in\left(SBD\right)\Rightarrow SG\in\left(SBD\right)\)
Trong mp (SCN), nối SG cắt MN tại H
\(\left\{{}\begin{matrix}H\in MN\\H\in SG\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow H=MN\cap\left(SBD\right)\)