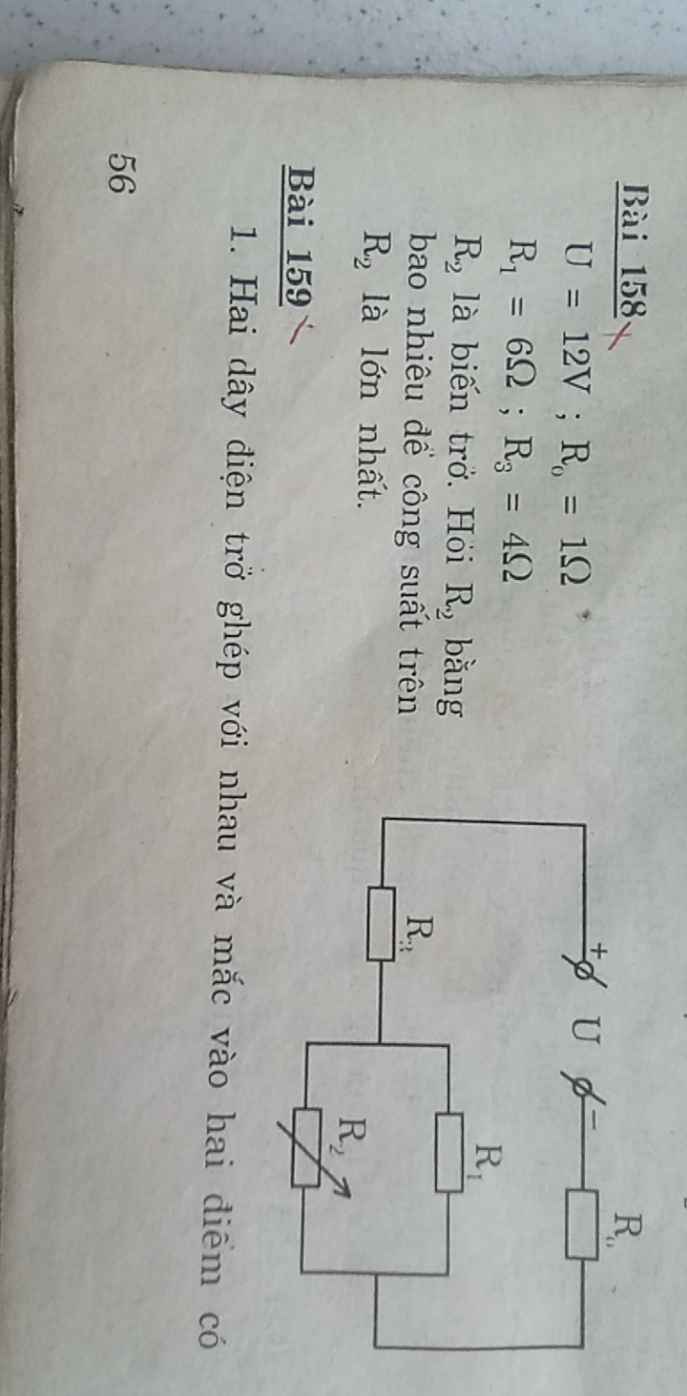
=>Ro nt R3 nt(R2//R1)(gọi R2 là x(ôm)
\(=>Rtd=Ro+R3+\dfrac{R1.x}{R1+x}=5+\dfrac{6x}{6+x}=\dfrac{11x+30}{6+x}\Omega\)
\(=>P2=\dfrac{U12^2}{R2}=\dfrac{\left(U-U3-U0\right)^2}{x}\)
\(=>P2=\dfrac{\left(12-ImR3-Im.Ro\right)^2}{x}=\dfrac{\left[12-Im\left(R3+Ro\right)\right]^2}{x}\)
\(=>P2=\dfrac{\left[12-\dfrac{12}{Rtd}.5\right]^2}{x}=\dfrac{\left[12-\dfrac{60\left(6+x\right)}{11x+30}\right]^2}{x}\)
\(=>P2=\dfrac{\left[\dfrac{132x+360-360-60x}{11x+30}\right]^2}{x}=\dfrac{\dfrac{\left(72x\right)^2}{\left(11x+30\right)^2}}{x}\)
\(=>P2=\dfrac{5184x^2}{\dfrac{x}{\left(11x+30\right)^2}}=\dfrac{5184x}{\left(11x+30\right)^2}\)
bĐT Cauchy \(=>\left(11x+30\right)^2\ge\left(2\sqrt{11.30x}\right)^2=1320x=>P\le\dfrac{5184}{1320}=3,9W\)
dấu"=" xảy ra tại x=2,7(ôm)=R2