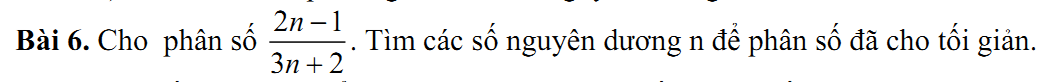Gọi \(d=ƯC\left(2n-1;3n+2\right)\Rightarrow\left\{{}\begin{matrix}2n-1⋮d\\3n+2⋮d\end{matrix}\right.\)
\(\Rightarrow2\left(3n+2\right)-3\left(2n-1\right)⋮d\)
\(\Rightarrow7⋮d\Rightarrow\left[{}\begin{matrix}d=1\\d=7\end{matrix}\right.\)
Với \(d=7\Rightarrow2n-1=7k\Rightarrow2\left(n-4\right)=7\left(k-1\right)\)
Do 2 và 7 nguyên tố cùng nhau \(\Rightarrow n-4⋮7\Rightarrow n-4=7m\)
\(\Rightarrow n=7m+4\)
Vậy với \(n=7m+4\) thì phân số đã cho không tối giản
\(\Rightarrow n\ne7m+4\) thì phân số đã cho tối giản \(\left(m\in N\right)\)