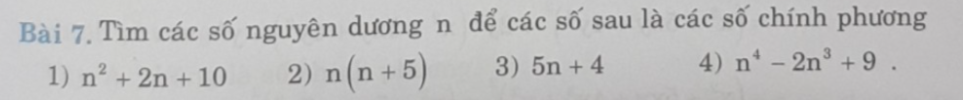Question

Answer 1

1.

Đặt $n^2+2n+10=a^2$ với $a$ là số tự nhiên 

$\Leftrightarrow (n+1)^2+9=a^2$

$\Leftrightarrow 9=a^2-(n+1)^2=(a+n+1)(a-n-1)$

Với $n$ nguyên dương, $a$ tự nhiên thì $a+n+1\in\mathbb{N}^*$. Mà $a+n+1> a-n-1$ nên $a+n+1=9; a-n-1=1$

$\Rightarrow n=3$
Hoàn toàn thỏa mãn

 

Answer 2

2. 

Đặt $n(n+5)=a^2$ với $a\in\mathbb{N}^*$

$4n(n+5)=4a^2$

$\Leftrightarrow 4n^2+20n=(2a)^2$

$\Leftrightarrow (2n+5)^2-25=(2a)^2$

$\Leftrightarrow (2n+5-2a)(2n+5+2a)=25$

Do $2n+5+2a\in\mathbb{N}^*$ và $2n+5+2a> 2n+5-2a$ nên:

$2n+5+2a=25; 2n+5-2a=1$

$\Rightarrow 2n+5=(25+1):2=13$

$\Rightarrow n=4$

Answer 3

3.

Đặt $5n+4=a^2$ với $a\in\mathbb{N}^*$

Ta có: $a^2=5n+4\equiv 4\pmod 5$

$\Leftrightarrow (a-2)(a+2)\equiv 0\pmod 5$

$\Rightarrow a-2\equiv 0\pmod 5$ hoặc $a+2\equiv 0\pmod 5$

Nếu $a-2\equiv 0\pmod 5$ thì đặt $a=5k+2$ với $k$ tự nhiên 

$5n+4=(5k+2)^2=25k^2+20k+4$
$\Leftrightarrow n=5k^2+4k$

Nếu $a+2\equiv 0\pmod 5$ thì $a=5k+3$ với $k$ tự nhiên 

$\Rightarrow 5n+4=(5k+3)^2=25k^2+30k+9$

$\Rightarrow n=5k^2+6k+1$

Vậy $n=5k^2+6k+1$ hoặc $n=5k^2+4k$ với $k$ là số tự nhiên.

 

Answer 4

4.

Xét hiệu:
$n^4-2n^3+9-(n^2-n+3)^2=6n-7n^2=n(6-7n)< 0$ với mọi $n\in\mathbb{N}^*$

$\Rightarrow n^4-2n^3+9< (n^2-n+3)^2$

Xét hiệu: 

$n^4-2n^3+9-(n^2-n-1)^2=n^2-2n+8=(n-1)^2+7>0$ với  mọi $n\in\mathbb{N}^*$

$\Rightarrow n^4-2n^3+9> (n^2-n-1)^2$

Vậy $(n^2-n+3)^2> n^4-2n^3+9> (n^2-n-1)^2$
Do đó để $n^4-2n^3+9$ là scp thì:

$n^4-2n^3+9=(n^2-n+2)^2(1)$ hoặc $n^4-2n^3+9=(n^2-n+1)^2(2)$ hoặc $n^4-2n^3+9=(n^2-n)^2(3)$

TH $(1)\Leftrightarrow -5n^2+4n+5=0$

$\Leftrightarrow n=\frac{2\pm \sqrt{29}}{5}$ (loại)

TH $(2)\Leftrightarrow -3n^2+2n+8=0$

$\Leftrightarrow n=2$ (chọn) hoặc $n=\frac{-4}{3}$ (loại)

TH $(3)\Leftrightarrow 9-n^2=0$

$\Leftrightarrow n=3$ (chọn) hoặc $n=-3$ (loại)

Vậy............