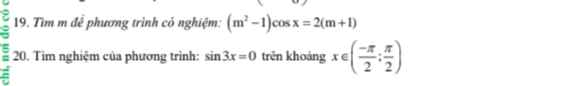\(\left(m^2-1\right)cosx=2\left(m+1\right)\) (1)
Xét \(m^2-1=0\)\(\Leftrightarrow m=\pm1\)
Tại m=1. PT (1) \(\Leftrightarrow0=2\left(1+1\right)=4\left(L\right)\)
Tại m=-1.PT (1)\(\Leftrightarrow0=0\left(lđ\right)\)
\(\Rightarrow m=-1\) thỏa mãn và \(m=1\) ktm (I)
Xét \(m^2-1\ne0\)\(\Leftrightarrow m\ne\pm1\)
PT (1)\(\Leftrightarrow cosx=\dfrac{2\left(m+1\right)}{m^2-1}=\dfrac{2}{m-1}\)
Có \(cosx\in\left[-1;1\right]\)
Để pt (1) có nghiệm\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{m-1}\ge-1\\\dfrac{2}{m-1}\le1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{m-1}+1\ge0\\\dfrac{2}{m-1}-1\le0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{m+1}{m-1}\ge0\\\dfrac{3-m}{m-1}\le0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m\le-1\\m>1\end{matrix}\right.\\\left[{}\begin{matrix}m< 1\\m\ge3\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}m\le-1\\m\ge3\end{matrix}\right.\) (II)
Từ (I) và (II) \(\Rightarrow\left[{}\begin{matrix}m\le-1\\m\ge3\end{matrix}\right.\)
Vậy...
\(sin3x=0\)\(\Leftrightarrow x=\dfrac{k\pi}{3}\left(k\in Z\right)\)
Mà \(x\in\left(\dfrac{-\pi}{2};\dfrac{\pi}{2}\right)\)\(\Rightarrow\left\{{}\begin{matrix}\dfrac{k\pi}{3}>-\dfrac{\pi}{2}\\\dfrac{k\pi}{3}< \dfrac{\pi}{2}\end{matrix}\right.\) \(\Leftrightarrow k\in\left(\dfrac{-3}{2};\dfrac{3}{2}\right)\) mà \(k\in Z\)
\(\Rightarrow k\in\left\{-1;0;1\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{3}\\x=0\\x=\dfrac{\pi}{3}\end{matrix}\right.\)
Vậy...