Bài `4`.

`a,`

`AB^2+AD^2=BD^2` (Pytago)

`=> 15^2+8^2=BD^2`

`=> BD^2=289`

`=> BD=17` (cm)

`DA^2=DH.DB` (htlg)

`=> 8^2=DH.17`

`=> DH=64/17` (cm)

`BA^2=BH.BD` (htlg)

`=> 15^2=BH.17`

`=> BH=225/17`

`HA^2=HB.HD` (htlg)

`=> HA^2=225/17 . 64/17`

`=> HA=15 . 8/17=120/17` (cm)

`b,`

Xét `\triangle DHK` và `\triangle IHB` có:

`\hat{DHK}=90^o`

`\hat{HDK}=\hat{HIB}` (cùng phụ `\hat{HKD}=\hat{CKI}`)

Nên `\triangle DHK` $\backsim$ `\triangle IHB`

`c,`

Từ câu `b`, suy ra `(HK)/(HB)=(DH)/(IH)`

`=> HI.HK=HB.HD`

Mà `HB.HD=AH^2` (htlg)

`=> HA^2=HI.HK` (đpcm)

Câu 11: Ta có: $f(x)+f\bigg(\dfrac{x+1}{1-3x}\bigg)=x,$ $\forall x\ne\pm\dfrac{1}{3}$ $(1)$

Thế $x\rightarrow\dfrac{x+1}{1-3x}$ vào $(1)$, ta được: 

$f\bigg(\dfrac{x+1}{1-3x}\bigg)+f\bigg(\dfrac{x-1}{3x+1}\bigg)=\dfrac{x+1}{1-3x},$ $\forall x\ne\pm\dfrac{1}{3}$ $(2)$

Thế $x\rightarrow\dfrac{x-1}{3x+1}$ vào $(1)$, ta được: 

$f\bigg(\dfrac{x-1}{3x+1}\bigg)+f(x)=\dfrac{x-1}{3x+1},$ $\forall x\ne\pm\dfrac{1}{3}$ $(3)$

Cộng $(1)$, $(2)$ và $(3)$ vế theo vế rồi chia cả 2 vế cho `2` ta có:

$f(x)+f\bigg(\dfrac{x+1}{1-3x}\bigg)+f\bigg(\dfrac{x-1}{3x+1}\bigg)=\dfrac{x+\dfrac{x+1}{1-3x}+\dfrac{x-1}{3x+1}}{2},$ $\forall x\ne\pm\dfrac{1}{3}$

$⇒f(x)=\dfrac{9x^3+6x^2-x+2}{18x^2-2},$ $\forall x\ne\pm\dfrac{1}{3}$

Câu 13: Ta có: $f(2x+1)+2g(2x+1)=2x,$ $\forall x\ne1$

Thế $x\rightarrow\dfrac{x-1}{2}$, ta được: $f(x)+2g(x)=x-1,$ $\forall x\ne1$

Mặt khác, $f\bigg(\dfrac{x}{x-1}\bigg)+g\bigg(\dfrac{x}{x-1}\bigg)=x,$ $\forall x\ne1$

Thế $x\rightarrow\dfrac{x}{x-1}$, ta được: $f(x)+g(x)=\dfrac{x}{x-1},$ $\forall x\ne1$

Từ đó, ta dễ dàng suy ra được: 

$\begin{cases} f(x)=-x+1-\dfrac{2x}{x-1}\\g(x)=x-1-\dfrac{x}{x-1}\end{cases},$ $\forall x\ne1$

Câu 1: Thế nào là quần xã sinh vật? ví dụ nào sau đây là QXSV vì sao?

b. Rừng Cúc Phương.

Quần xã sinh vật là 1 tập hợp gồm nhiều quần thể sinh vật, có mỗi quan hệ dinh dưỡng và cùng tồn tại trong 1 khoảng thời gian và không gian

Câu 2: Sắp xếp các loài động vật sau theo trình tự tiến hóa từ thấp đến cao: Chim bồ câu, Giun đũa, Cá chép, Thằn lằn, Châu chấu

Giun đũa=>châu chấu=>cá chép=>thằn lằn=>chim bồ câu

Câu 3: Nêu chức năng của các hệ cơ quan sau

a. hô hấp.=>Cung cấp oxy và đào thải CO2

b. bài tiết.=>Bài tiết các chất dư thừa và sản phẩm độc hại

c. tiêu hóa.=>Tiêu hóa và hấp thu chất dinh dưỡng

d. tuần hoàn.=> Vận chuyển các chất đi nuôi dưỡng cơ thể và lấy đi các chất dư thừa độc hại 

Câu 4: Phương trình sau đây biểu diễn một hoạt động sống của tế bào nào? Vì sao? CO2 + H2O (ánh sáng mặt trời)/> O2 + C6H12O6.

Tế bào lạp thể vì đây là quá trình quang hợp ở TV

Câu 5: Cơ chế di truyền ở cấp độ phân tử là gì?

- Sao chép ADN

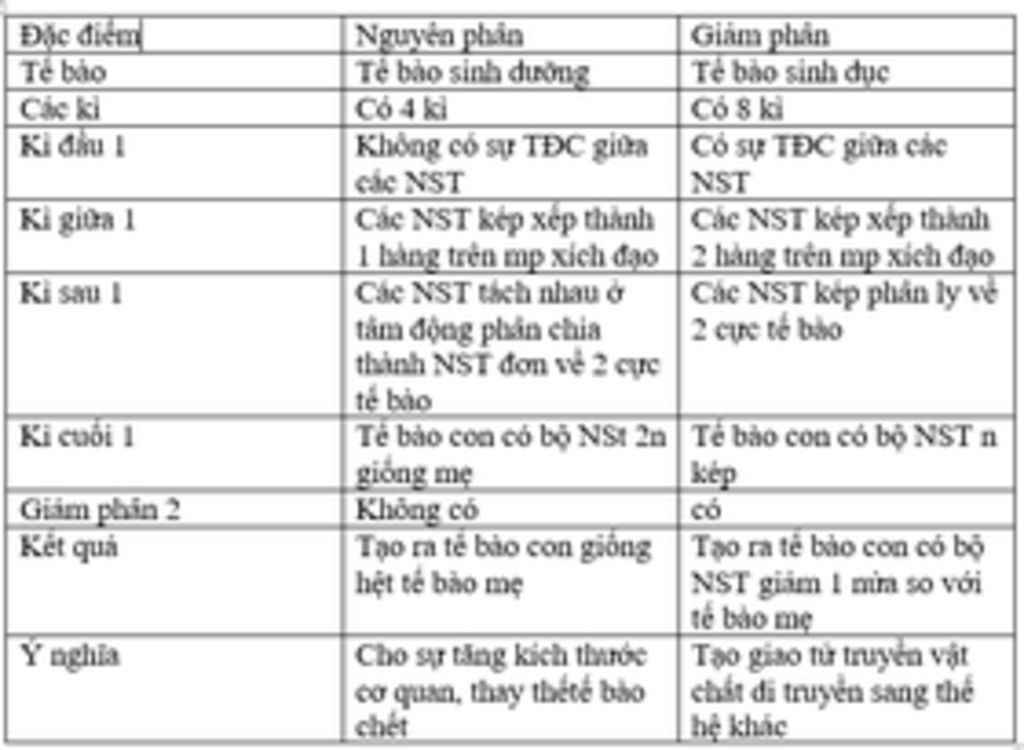
Câu 6: So sánh chỉ ra sự khác biệt về diễn biến NST qua các kì của quá trình phân bào ở tế bào mầm sinh dục và tế bào sinh dục chín trên cơ thể động vật.

Câu 7: Xét một tế bào mang gen B (dài 4080Å). Sau nguyên phân thu được một số tế bào mang gen B’ (biến đổi từ B) có chiều dài 4083,4Å. a. Tính số gen B’ thu được sau 4 lần phân bào? Xác định dạng đột biến xảy ra? b. Giải thích nguyên nhân, tính chất, vai trò của sự xuất hiện B’ từ B. (Giả sử rối loạn xảy ra ở ngay lần nguyên phân đầu tiên của tế bào đang xét)

Số gen B' thu được: 2^4=16 gen

Dạng đột biến:

Gen B' dài hơn gen B 3,4 angtron

=>đột biến thêm 1 cặp nu

Nguyên nhân:

Do sự bắt cặp nhẫm lẫn của các cặp nu

Tính chất: làm xuất hiện thêm 1 cặp nu

Vai trò: Thay đổi mã di truyền kể từ nu bị lặp

Câu 1 sai vì trong hệ tiêu hóa của trâu bò ko có enzim phân giải xenlulose

Câu 2 sai vì pepsin của trâu bò cũng ko tiêu hóa được xenlulose

Câu 3 sai vì vi khuẩn tiêu hóa ở trâu bò ko cộng sinh trong manh tràng mà cộng sinh trong dạ cỏ

Câu 4 đúng vì trâu bò ko  có enzim phân giải xenlulose => vi sinh vật trong dạ dày ( đặc biệt là dạ cỏ) của bò làm việc này

Câu 5 đúng dạ dày của trâu bò phù hợp với việc nhai lại và để tiêu hóa các loại thức ăn kém dinh dưỡng như cỏ

Câu 6 sai  vì trâu bò không có răng nanh

Câu 7 sai vi sinh vật cộng sinh giúp trâu bò tiêu hóa chất xơ chứ ko phải là thức ăn của trâu bò

Câu 8 sai trâu bò ko cần sỏi để nghiền thức ăn

a) `M_(X)=M_(H_2).44=2.44=88`$g/mol$ `n_(X)=(8,8)/88=0,1mol` `X` sẽ là este no, đơn chức mạch hở có dạng tổng quát: `RCOOR'` PTHH: `RCOOR'+NaOH->RCOONa+R'OH` `M_(Y)=16.M_(H_2)=16.2=32`$g/mol$ `32` sẽ là khối lượng mol của `R'OH` vì nếu của `RCOONa` sẽ không phù hợp vì `M=44+23=67` (Chưa tính `M_(R)`) `R'OH` là ancol no đơn chức mạch hở. `M_(R')+M_(OH)=32` `<=>M_(R')+17=32` `->M_(R')=15(CH_3)` `M_(RCOOR')=M_(R)+44+15=88` `->M_(R)=29`(`C_2H_5`) Vậy `X` có công thức là `C_2H_5COOCH_3`: Metyl propionat b) `C_2H_5COOCH_3+NaOH->C_2H_5COONa+CH_3OH` `0,1.......................................→0,1mol` `->m_(C_2H_5COONa)=0,1.96=9,6g`

Thang máy đi xuống đều ⇒ Gia tốc bằng 0 `(a_0=0)`

⇒ Gia tốc hiệu dụng:

`\vec{g}_{hd}=\vec{g}+\vec{a_0}=\vec{g}`

⇒ Chu kì dao động của con lắc:

`T_{hd}=2π\sqrt{\frac{l}{g_{hd}}}=2π\sqrt{\frac{l}{g}}=T`

⇔ `f_{hd}=f=1/T=1/2=0,5 \ (Hz)`

a) Ta có:

`SA⊥(ABCD) ⇒ SA⊥AO`

⇒ `AO` là hình chiếu của `SO` lên `(ABCD)`

⇒ `∠(SO;(ABCD))=∠(SO;AO)=∠SOA=45^o`

`AC=\sqrt{AB^2+BC^2}=\sqrt{a^2+3a^2}=2a`

⇒ `AO=\frac{AC}{2}=a/2`

`SA=AO\tanSOA=a\tan45^o=a`

Vậy `V_{S.ABCD}=\frac{1}{3}SA.ABCD=\frac{1}{3}a.a.a\sqrt{3}=\frac{a^3\sqrt{3}}{3}`

b) `S_{ΔOCD}=\frac{1}{2}.\frac{1}{2}BC.AB=\frac{1}{4}.a\sqrt{3}.a=\frac{a^2\sqrt{3}}{4}`

`V_{S.OCD}=\frac{1}{3}SA.S_{ΔOCD}=\frac{1}{3}.a.\frac{a^2\sqrt{3}}{4}=\frac{a^3\sqrt{3}}{12}`

c) Kẻ $IH \ // \ SA \ (H∈AD) ⇒ IH⊥(ABCD)$

Hay `IH⊥(OBC)`

Ta có:

`S_{ΔOBC}=\frac{1}{2}.\frac{1}{2}AB.BC=\frac{1}{4}.a.a\sqrt{3}=\frac{a^2\sqrt{3}}{4}`

Vì `I` là trung điểm của `SD` nên `IH=\frac{SA}{2}=a/2`

Vậy `V_{I.OBC}=\frac{1}{3}IH.S_{ΔOBC}=\frac{1}{3}.\frac{a}{2}.\frac{a^2\sqrt{3}}{4}=\frac{a^3\sqrt{3}}{24}`

$\begin{array}{l}
\sin 2x + 2\cos x + 5\sin x + 5 = 0\\
 \Leftrightarrow 2\sin x\cos x + 2\cos x + 5\left( {\sin x + 1} \right) = 0\\
 \Leftrightarrow 2\cos x\left( {\sin x + 1} \right) + 5\left( {\sin x + 1} \right) = 0\\
 \Leftrightarrow \left( {\sin x + 1} \right)\left( {2\cos x + 5} \right) = 0\\
 \Leftrightarrow \left[ \begin{array}{l}
\sin x =  - 1\\
\cos x =  - \dfrac{5}{2}(L)
\end{array} \right. \Leftrightarrow x =  - \dfrac{\pi }{2} + k2\pi \left( {k \in Z} \right)\\
b){\cos ^3}x - {\sin ^3}x = \cos 2x\\
 \Leftrightarrow \left( {\cos x - \sin x} \right)\left( {{{\cos }^2}x + {{\sin }^2}x + \cos x\sin x} \right) = \left( {\cos x - \sin x} \right)\left( {\cos x + \sin x} \right)\\
 \Leftrightarrow \left( {\cos x - \sin x} \right)\left( {1 - \sin x - \cos x - \sin x\cos x} \right) = 0\\
 \Leftrightarrow \left( {\cos x - \sin x} \right)\left( {\sin x + \cos x + \sin x\cos x - 1} \right) = 0\\
 \Leftrightarrow \left[ \begin{array}{l}
\cos x = \sin x\\
\sin x + \cos x + \sin x\cos x = 1
\end{array} \right.\\
 \Leftrightarrow \left[ \begin{array}{l}
\sqrt 2 \cos \left( {x + \dfrac{\pi }{4}} \right) = 0\\
t + \dfrac{{{t^2} - 1}}{2} = 1\left( {t = \sin x + \cos x, - \sqrt 2  \le t \le \sqrt 2 } \right)
\end{array} \right.\\
 \Leftrightarrow \left[ \begin{array}{l}
x + \dfrac{\pi }{4} = \dfrac{\pi }{2} + k\pi \\
{t^2} + 2t - 1 = 0
\end{array} \right.\\
 \Leftrightarrow \left[ \begin{array}{l}
x = \dfrac{\pi }{4} + k\pi \\
t =  - 1 - \sqrt 2 (L)\\
t = \sqrt 2  - 1
\end{array} \right.\\
 \Rightarrow \left[ \begin{array}{l}
x = \dfrac{\pi }{4} + k\pi \\
\sqrt 2 \sin \left( {x + \dfrac{\pi }{4}} \right) = \sqrt 2  - 1
\end{array} \right.\\
 \Leftrightarrow \left[ \begin{array}{l}
x = \dfrac{\pi }{4} + k\pi \\
\sin \left( {x + \dfrac{\pi }{4}} \right) = 1 - \dfrac{{\sqrt 2 }}{2}
\end{array} \right.\\
 \Leftrightarrow \left[ \begin{array}{l}
x = \dfrac{\pi }{4} + k\pi \\
x + \dfrac{\pi }{4} = \arcsin \left( {1 - \dfrac{{\sqrt 2 }}{2}} \right) + k2\pi \\
x + \dfrac{\pi }{4} = \pi  - \arcsin \left( {1 - \dfrac{{\sqrt 2 }}{2}} \right) + k2\pi 
\end{array} \right.\left( {k \in \mathbb Z} \right)
\end{array}$

Câu 38: ĐKXĐ: `x-m#0; <=> m # x`

Mà `x ∈ (2; +∞); => m ∈ (-∞; 2]` hay `m ≤ 2`             `(1)`

Ta có: `y^' = (-m-1)/(x-m)^2`

Để hàm số nghịch biến; `=> -m-1 < 0; <=> m > -1`           `(2)`

Kết hợp `(1)` và `(2)` `=> -1 < m ≤ 2`

`=>` Giá trị nguyên của `m` là: `0; 1; 2`

`=>` Có `3` giá trị nguyên

`=>` Chọn `A`

---------------------------------------------------------------------------------------

Câu 39: Xét tam giác vuông `ABC`:

Theo định lý Pitago ta có:

`AC^2 + BC^2 = AB^2; <=> BC^2 = AB^2 - AC^2 = (asqrt3)^2 - a^2= 2a^2`

`=> BC = asqrt2`

`=> S_(ABC) = AC.BC : 2 = asqrt2 . a : 2= (a^2. sqrt2)/2`

Hai mặt phẳng `SAC` và `SAB` cùng vuông góc với đáy

`=>\ SA` vuông góc với đáy; `=> SA ⊥ (ABC); => SA ⊥ AC`

`=>` Tam giác `SAC` vuông tại `A`

Theo định lý Pitago: `SA^2+AC^2 = SC^2;`

`<=> SA^2= SC^2-AC^2 =(a sqrt5)^2 - a^2 = 4a^2; => SA = 2a`

Thể tích khối chóp `S.ABC` là: `S_(ABC) .  SA . 1/3`

`= (a^2. sqrt2)/2 . 2a . 1/3 = (a^3 sqrt2)/3`

`=>` Chọn `C`

tham khảo hình

$\left( {{x}^{2}}y-8x+y-3 \right){{\log }_{9}}y={{\log }_{3}}\dfrac{\sqrt{8x-y+4}}{x}\,\,\,\left( * \right)$

Điều kiện: $y>0$ và $8x-y+4>0$

Do $x>1$ nên $8x+4>12$

Mà $8x-y+4>0$

Nên nếu $0<y\le 12$ thì chắc chắn thỏa mãn điều kiện xác định

$\left( * \right)\Leftrightarrow \left[ {{x}^{2}}y+1-\left( 8x-y+4 \right) \right]{{\log }_{3}}y={{\log }_{3}}\dfrac{8x-y+4}{{{x}^{2}}}$

$\Leftrightarrow {{x}^{2}}y{{\log }_{3}}y+{{\log }_{3}}y-\left( 8x-y+4 \right){{\log }_{3}}y={{\log }_{3}}\left( 8x-y+4 \right)-{{\log }_{3}}{{x}^{2}}$

$\Leftrightarrow {{x}^{2}}y{{\log }_{3}}y+\left( {{\log }_{3}}{{x}^{2}}+{{\log }_{3}}y \right)=\left( 8x-y+4 \right){{\log }_{3}}y+{{\log }_{3}}\left( 8x-y+4 \right)$

$\Leftrightarrow {{x}^{2}}y{{\log }_{3}}y+{{\log }_{3}}\left( {{x}^{2}}y \right)=\left( 8x-y+4 \right){{\log }_{3}}y+{{\log }_{3}}\left( 8x-y+4 \right)$

$\Leftrightarrow {{x}^{2}}y=8x-y+4$(hàm đặc trưng, đồng biến $f\left( t \right)=t{{\log }_{3}}y+{{\log }_{3}}t$))

$\Leftrightarrow y=\dfrac{8x+4}{{{x}^{2}}+1}$

Xét $y=f\left( x \right)=\dfrac{8x+4}{{{x}^{2}}+1}$

$\Rightarrow f'\left( x \right)=\dfrac{-8{{x}^{2}}-8x+8}{{{\left( {{x}^{2}}+1 \right)}^{2}}}$

Cho $f\left( x \right)=0\Leftrightarrow x=\dfrac{-1\pm \sqrt{5}}{2}$ (không thỏa mãn $x>1$)

Bảng biến thiên: Xem hình

Dựa vào bảng biến thiên

Để $f\left( x \right)$ có nghiệm

Thì $0<y<6$

$\Rightarrow y\in \left\{ 1;2;3;4;5 \right\}$ (thỏa mãn điều kiện)

Vậy có $5$ giá trị nguyên dương của $y$

Chọn câu $A$