Cho hai khối hộp chữ nhật: khối hộp thứ nhất có ba kích thước x, 2x và 3y; khối hộp thứ hai có diện tích đáy là 2xy. Tính chiều cao (cạnh bên) của khối hộp thứ hai, biết rằng hai khối hộp có cùng thể tích.
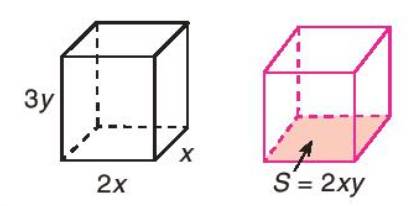
Cho hai khối hộp chữ nhật: khối hộp thứ nhất có ba kích thước x, 2x và 3y; khối hộp thứ hai có diện tích đáy là 2xy. Tính chiều cao (cạnh bên) của khối hộp thứ hai, biết rằng hai khối hộp có cùng thể tích.

Hãy nhớ lại cách chia đơn thức cho đơn thức trong trường hợp chúng có một biến và hoàn thành các yêu cầu sau:
a) Thực hiện phép chia \(6{x^3}:3{x^2}\).
b) Với \(a,b \in \mathbb{R}\) và \(b \ne 0;m,n \in \mathbb{N}\), hãy cho biết:
Khi nào thì \(a{x^m}\) chia hết cho \(b{x^n}\).Nhắc lại cách thực hiện phép chia \(a{x^m}\) cho \(b{x^n}\).
Thảo luận (1)Hướng dẫn giảia) \(6{x^3}:3{x^2} = \left( {6:3} \right).\left( {{x^3}:{x^2}} \right) = 2x\)
b) * Khi \(m \ge n\)
* Để chia \(a{x^m}\) cho \(b{x^n}\) ta thực hiện phép chia a:b và \({x^m}:{x^n}\) rồi nhân 2 kết quả với nhau.
(Trả lời bởi Hà Quang Minh)
Với mỗi trường hợp sau, hãy đoán xem đơn thức A có chia hết cho đơn thức B không; nếu chia hết, hãy tìm thương của phép chia A cho B và giải thích cách làm:
a) \(A = 6{x^3}y,B = 3{x^2}y\)
b) \(A = {x^2}y,B = x{y^2}\)
Thảo luận (1)Hướng dẫn giảia) Đơn thức A chia hết cho đơn thức B:
\(A:B = 6{x^3}y:3{x^2}y = \left( {6:3} \right).\left( {{x^3}:{x^2}} \right).\left( {y:y} \right) = 2x\)
b) Đơn thức A không chia hết cho đơn thức B vì số mũ của biến y trong B lớn hơn số mũ của biến y trong A.
(Trả lời bởi Hà Quang Minh)
Trong các phép chia sau đây, phép chia nào không là phép chia hết? Tại sao? Tìm thương của các phép chia còn lại:
a) \( - 15{x^2}{y^2}\) chia cho \(3{x^2}y\);
b) \(6xy\) chia cho \(2yz\);
c) \(4x{y^3}\) chia cho \(6x{y^2}\).
Thảo luận (1)Hướng dẫn giảia)
\( - 15{x^2}{y^2}:3{x^2}y = \left( { - 15:3} \right).\left( {{x^2}:{x^2}} \right):\left( {{y^2}:y} \right) = - 5y\)
b)
Không là phép chia hết vì số mũ của biến z trong \(2yz\) lớn hơn số mũ của biến z trong \(6xy\).
c)
\(4x{y^3}:6x{y^2} = \left( {4:6} \right).\left( {x:x} \right).\left( {{y^3}:{y^2}} \right) = \dfrac{2}{3}y\)
(Trả lời bởi Hà Quang Minh)
Cho hai khối hộp chữ nhật: khối hộp thứ nhất có ba kích thước x, 2x và 3y; khối hộp thứ hai có diện tích đáy là 2xy. Tính chiều cao (cạnh bên) của khối hộp thứ hai, biết rằng hai khối hộp có cùng thể tích.
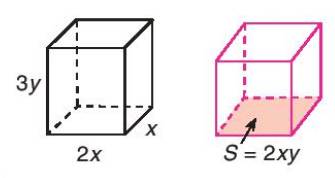
Thảo luận (1)Hướng dẫn giảiThể tích của khối hộp thứ nhất là: 2x . x . 3y = 6x2y.
Vì hai khối hộp có cùng thể tích nên khối hộp thứ hai có thể tích 6x2y.
Chiều cao của khối hộp thứ hai là: 6x2y : 2xy = 3x.
Vậy chiều cao (cạnh bên) của khối hộp thứ hai là 3x.
(Trả lời bởi Quoc Tran Anh Le)
Làm tính chia \(\left( {6{x^4}{y^3} - 8{x^3}{y^4} + 3{x^2}{y^2}} \right):2x{y^2}\)
Thảo luận (1)Hướng dẫn giải\(\dfrac{6x^4y^3-8x^3y^4+3x^2y^2}{2xy^2}=\dfrac{6x^4y^3}{2xy^2}-\dfrac{8x^3y^4}{2xy^2}+\dfrac{3x^2y^2}{2xy^2}=3x^3y-4x^2y^2+\dfrac{3}{2}x\)
(Trả lời bởi Hà Quang Minh)
Tìm đa thức A sao cho \(A.\left( { - 3xy} \right) = 9{x^3}y + 3x{y^3} - 6{x^2}{y^2}\)
Thảo luận (1)Hướng dẫn giải\(\begin{array}{l}A.\left( { - 3xy} \right) = 9{x^3}y + 3x{y^3} - 6{x^2}{y^2}\\ \Rightarrow A = \left( {9{x^3}y + 3x{y^3} - 6{x^2}{y^2}} \right):\left( { - 3xy} \right)\\ = 9{x^3}y:\left( { - 3xy} \right) + 3x{y^3}:\left( { - 3xy} \right) - 6{x^2}{y^2}:\left( { - 3xy} \right)\\ = - 3{x^2} - {y^2} + 2xy\end{array}\)
(Trả lời bởi Hà Quang Minh)
a) Tìm đơn thức M biết rằng \(\dfrac{7}{3}{x^3}{y^2}:M = 7x{y^2}\)
b) Tìm đơn thức N biết rằng \(N:0,5x{y^2}z = - xy\)
Thảo luận (1)Hướng dẫn giảia)
\(\begin{array}{l}\dfrac{7}{3}{x^3}{y^2}:M = 7x{y^2}\\ \Rightarrow M = \dfrac{7}{3}{x^3}{y^2}:7x{y^2} = \left( {\dfrac{7}{3}:7} \right).\left( {{x^3}:x} \right).\left( {{y^2}:{y^2}} \right) = \dfrac{1}{3}{x^2}\end{array}\)
b)
\(\begin{array}{l}N:0,5x{y^2}z = - xy\\ \Rightarrow N = \left( { - xy} \right).0,5x{y^2}z = \left( { - 0,5} \right).\left( {x.x} \right).\left( {y.{y^2}} \right).z = - 0,5{x^2}{y^3}z\end{array}\)
(Trả lời bởi Hà Quang Minh)
Cho đa thức \(A = 9x{y^4} - 12{x^2}{y^3} + 6{x^3}{y^2}\). Với mỗi trường hợp sau đây, xét xem A có chia hết cho đơn thức B hay không? Thực hiện phép chia trong trường hợp A chia hết cho B.
a) \(B = 3{x^2}y\)
b) \(B = - 3x{y^2}\)
Thảo luận (1)Hướng dẫn giảia) Không vì hạng tử \( 9x{y^4}\) có số mũ của biến x nhỏ hơn số mũ của biến x trong B.
b) Có. \(\begin{array}{l}A:B = \left( {9x{y^4} - 12{x^2}{y^3} + 6{x^3}{y^2}} \right):\left( { - 3x{y^2}} \right)\\ = 9x{y^4}:\left( { - 3x{y^2}} \right) - 12{x^2}{y^3}:\left( { - 3x{y^2}} \right) + 6{x^3}{y^2}:\left( { - 3x{y^2}} \right)\\ = - 3{y^2} + 4xy - 2{x^2}\end{array}\)
(Trả lời bởi Hà Quang Minh)
Thực hiện phép chia \(\left( {7{y^5}{z^2} - 14{y^4}{z^3} + 2,1{y^3}{z^4}} \right):\left( { - 7{y^3}{z^2}} \right)\)
Thảo luận (1)Hướng dẫn giải\(\begin{array}{l}\left( {7{y^5}{z^2} - 14{y^4}{z^3} + 2,1{y^3}{z^4}} \right):\left( { - 7{y^3}{z^2}} \right)\\ = 7{y^5}{z^2}:\left( { - 7{y^3}{z^2}} \right) - 14{y^4}{z^3}:\left( { - 7{y^3}{z^2}} \right) + 2,1{y^3}{z^4}:\left( { - 7{y^3}{z^2}} \right)\\ = - {y^2} + 2yz - 0,3{z^2}\end{array}\)
(Trả lời bởi Hà Quang Minh)