Bài 2: Tỉ số lượng giác của góc nhọn
Các câu hỏi tương tự
\(B=\left(1+\tan^2\right)\left(1-\sin^2\right)-\left(1+cotan^2\right)\left(1-\cos^2\right)\)
1/Cho góc nhọn x. Hãy rút gọn các biểu thức sau:
a)\(sin^4x+cos^4x+2sin^2x.cos^2x\)
b)\(tan^2x\left(2cos^2x+sin^2x-1\right)\)
c)\(\left(1+tan^2x\right)\left(1-sin^2x\right)-\left(1+cot^2x\right)\left(1-cos^2\right)\)
Rút gọn biểu thức:
\(A=\sin^210+\sin^220+\sin^230+\sin^280+\sin^270+\sin^260\)
\(B=\left(1+\tan^2\alpha\right)\left(1-\sin^2\alpha\right)+\left(1+\cot^2\alpha\right)\left(1-\cos^2\alpha\right)\)
Cho 0o x 90o, CM các biểu thức sau không phụ thuộc vào biến:
1.A2left(sin^4x+cos^4x+sin^2xcos^2xright)^2-left(sin^8x+cos^8xright)
2.Bleft(dfrac{1-tan^2x}{tan x}right)^2-left(1+tan^2xright)left(1+cot^2xright)
3.Cleft(sin^4x+cos^4x-1right)left(tan^2x+cot^2x+2right)
4.Ddfrac{tan^2x-cos^2x}{sin^2x}+dfrac{cot^2x-sin^2x}{cos^2x}
5.Edfrac{cot^2x-cos^2x}{cot^2x}+dfrac{sin xcdotcos x}{cot x}
Đọc tiếp
Cho 0o < x < 90o, CM các biểu thức sau không phụ thuộc vào biến:
\(1.A=2\left(\sin^4x+\cos^4x+\sin^2x\cos^2x\right)^2-\left(\sin^8x+\cos^8x\right)\)
\(2.B=\left(\dfrac{1-\tan^2x}{\tan x}\right)^2-\left(1+\tan^2x\right)\left(1+\cot^2x\right)\)
\(3.C=\left(\sin^4x+\cos^4x-1\right)\left(\tan^2x+\cot^2x+2\right)\)
\(4.D=\dfrac{\tan^2x-\cos^2x}{\sin^2x}+\dfrac{\cot^2x-\sin^2x}{\cos^2x}\)
\(5.E=\dfrac{\cot^2x-\cos^2x}{\cot^2x}+\dfrac{\sin x\cdot\cos x}{\cot x}\)
Trong mặt phẳng tọa độ, các đỉnh của tam giác ABC có tọa độ như sau :
\(A\left(1;1\right),B\left(5;1\right),C\left(7;9\right)\), (h.11). Hãy tính :
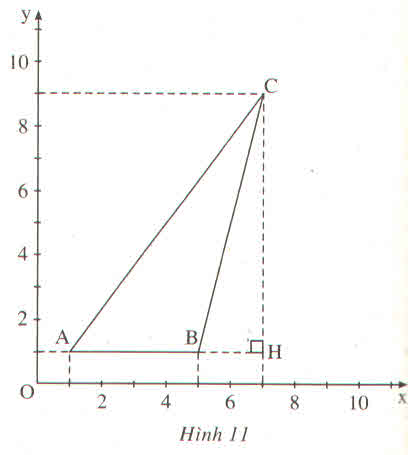
a) Giá trị của \(tg\widehat{BAC}\) (làm tròn đến chữ số thập phân thứ tư)
b) Độ dài cạnh AC
chứng minh 4 = \(\dfrac{\left(sin+cos\right)^2-\left(sin-cos\right)^2}{sin\cdot cos}\)
D = \(\dfrac{\left(\sin\alpha+\cos\alpha\right)^2-\left(\sin\alpha-\cos\alpha\right)^2}{\sin\alpha\cdot\cos\alpha}\)
Giúp mk vs please![]()
Cho 0o < x < 90o, CM các biểu thức sau không phụ thuộc vào biến:
\(\left(\dfrac{1-\tan^2x}{\tan x}\right)^2-\left(1+\tan^2x\right).\left(1+\cot^2x\right)\)
Rút gọn .
\(A=\dfrac{1+2\sin\alpha\cos\alpha}{\sin\alpha+\cos\alpha}\)
\(B=\left(\sin\alpha+\cos\alpha\right)^2-\left(\cos\alpha-\sin\alpha\right)^2\)
\(C=\dfrac{\left(\sin\alpha-\cos\alpha\right)^2-\left(\sin\alpha+\cos\alpha\right)}{\sin\alpha\cos\alpha}\)
Mấy bạn giúp đỡ được phần nào thì giúp , giúp hết thì tốt quá .










