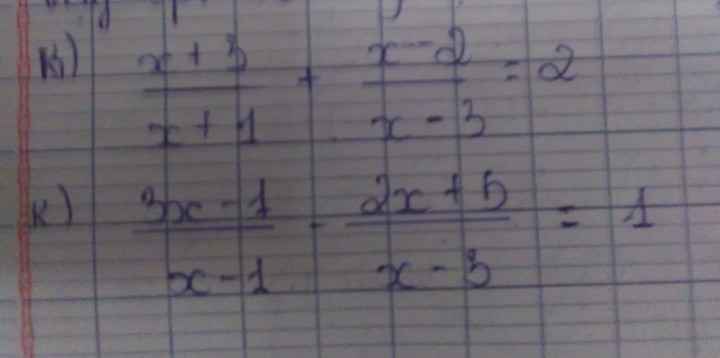Bài 5: Giải phương trình
a, \(=\dfrac{24x}{6}-\dfrac{4x}{6}+\dfrac{3\left(6-x\right)}{6}+\dfrac{3x}{6}=\dfrac{6\left(10-x\right)}{6}\)
\(\Leftrightarrow24x-4x+18-3x+3x=60-6x\)
\(\Leftrightarrow24x-4x-3x+3x+6x=60-18\\ \Leftrightarrow26x=42\\ \Leftrightarrow x=\dfrac{42}{26}=\dfrac{21}{13}\)
\(Vậy.S=\left\{\dfrac{21}{13}\right\}\)
b, \(=\dfrac{3.\left(x+2\right)}{6}=\dfrac{2.\left(2x-1\right)}{6}+\dfrac{6}{6}\\ \Leftrightarrow3x+6=4x-2+6\)
\(\Leftrightarrow3x-4x=6-2-6\\ \Leftrightarrow-1x=-2\\ \Leftrightarrow x=2\)
\(Vậy.S=\left\{2\right\}\)
c, \(\Leftrightarrow\dfrac{24}{12}-\dfrac{4.\left(2x+1\right)}{12}=\dfrac{12x}{12}-\dfrac{3\left(x-1\right)}{12}\\ \Leftrightarrow24-8x-4=12x-3x+3\)
\(\Leftrightarrow-8x-12x+3x=3-24+4\\ \Leftrightarrow-17x=-17\\ \Leftrightarrow x=1\\ Vậy.S=\left\{1\right\}\)
a: =>24x-16x+3(6-x)+3x=6(10-x)
=>8x+18=60-6x
=>14x=42
hay x=3
b: \(\Leftrightarrow\dfrac{x+2}{2}=\dfrac{2x-1+3}{3}\)
\(\Leftrightarrow\dfrac{x+2}{2}=\dfrac{2x+2}{3}\)
=>3x+6=4x+4
=>4x+4=3x+6
=>x=2
c: \(\Leftrightarrow\dfrac{6-2x-1}{3}=\dfrac{4x-x+1}{4}\)
\(\Leftrightarrow\dfrac{5-2x}{3}=\dfrac{3x+1}{4}\)
=>20-8x=9x+3
=>-17x=-17
hay x=1

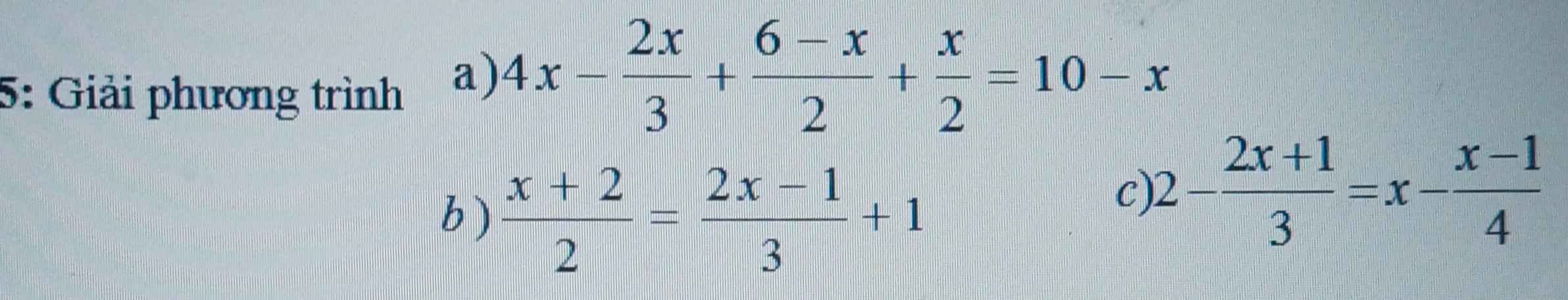









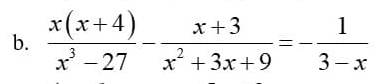 giúp mình với ạ
giúp mình với ạ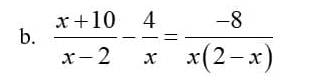 giúp mình với ạ
giúp mình với ạ